总结
二叉树篇,我们总共做了有关二叉树的遍历方式、求解二叉树的属性、对二叉树的修改以及构造等这几类的题型, 总结下来就是对二叉树的各种遍历方式的不同程度应用。
如果做到像对二叉树的递归遍历的每个层次都知道下一步要干什么、需要怎么回溯得到什么结果、 每层遍历得到的内容是什么下一层又会遍历到哪一个节点、如何记录前一个节点、递归终止的逻辑是什么……
对于迭代遍历如何确定是使用栈还是队列、队列or栈中的数是代表什么、出栈or入栈操作需要做的下一步是什么、如何收集结果、队列和递归的区别是什么…….
如果上述的几个问题你都能够全部想明白并且能够通过代码的方式实现, 那么二叉树章节基本是没有什么问题了。
题型题解
二叉树的遍历篇
二叉树的遍历篇已全部ac, 相关题目在卡哥的《代码随想录》中都有, 个人建议每个题目都用递归和迭代都做一边。
遍历的相关题型
二叉树的属性篇
二叉树的属性就是对二叉树的高度、路径、是否对称、是否相等、树的和、路径之和、左下角的值、右下角的值等等 一系列的围绕着二叉树遍历展开的题型
111.二叉树的最小深度
这道题和二叉树的最大深度有所不同, 所以做的时候容易踩坑
题目:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

返回它的最小深度 2.
实现思路
通过使用层序遍历的方式, 因为队列中存储的都是每一层的数据, 所以如果当前层的结果在出队列的时候不为叶子节点(左右子节点都为空的叫叶子节点),那么就给当前层数+1。反之退出遍历, 返回到当前层的层数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public int minDepth(TreeNode root) {
Queue<TreeNode> que = new LinkedList<>();
int depth = 0;
if(root == null) return depth;
que.offer(root);
while(!que.isEmpty()){
int len = que.size();
depth++;
while(len > 0){
TreeNode node = que.poll();
if(node.left != null) que.offer(node.left);
if(node.right!= null) que.offer(node.right);
if(node.left == null && node.right == null){
return depth;
}
len--;
}
}
return depth;
}
}
|
110. 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]

返回 true 。
实现思路
本题主要就是得到当前节点的两个子树的深度,然后通过深度相减得到判断是否为平衡二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| class Solution {
public boolean isBalanced(TreeNode root) {
Queue<TreeNode> que = new LinkedList<>();
if(root == null) return true;
que.offer(root);
while(!que.isEmpty()){
int len = que.size();
while(len > 0){
TreeNode node = que.poll();
int leftD = getDepth(node.left);
int rightD = getDepth(node.right);
if(leftD >rightD){
int res = leftD - rightD;
if(res > 1){
return false;
}
}else{
int res = rightD - leftD;
if(res > 1){
return false;
}
}
if(node.right!= null) que.offer(node.right);
if(node.left!=null) que.offer(node.left);
len--;
}
}
return true;
}
public int getDepth(TreeNode root){
if(root == null) return 0;
int leftD = getDepth(root.left);
int rightD = getDepth(root.right);
int depth = Math.max(leftD, rightD) + 1;
return depth;
}
}
|
257. 二叉树的所有路径
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
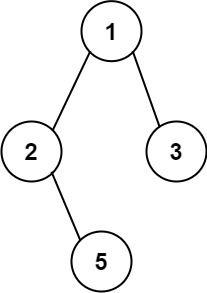
1
2
| 输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
|
示例 2:
实现思路
本题也没啥难度,唯一复杂点的地方就是在于路径的拼接, 如果到了路径的最后一个节点需要删除其的->
同时,还需要牢记回溯的步骤。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
List<String> res = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
if(root == null) return res;
List<Integer> path = new ArrayList<>();
combine(root, path, res);
return res;
}
public void combine(TreeNode node, List<Integer> path, List<String> res){
path.add(node.val);
if(node.left == null && node.right == null){
String str = "";
for(int i =0 ;i < path.size() - 1; i++){
str += path.get(i) ;
str += "->";
}
str += path.get(path.size() - 1);
res.add(str);
return;
}
if(node.left!=null){
combine(node.left, path,res);
path.remove(path.size() -1);
}
if(node.right != null){
combine(node.right, path, res);
path.remove(path.size() -1);
}
}
}
|
差不多对于二叉树的属性篇章也没什么太难的题型, 只需要注意相关细节即可AC, 重点在于二叉树的修改与构造。
二叉树的修改与构造篇
从最简单的来实现 就是 二叉树的反转(虽然最简单但是也难倒了大佬Max Howell)。
最简单的方式就是通过递归前序遍历, 然后swap两个子节点。
接下来就是通过前序和中序、中序和后序的结果来构造二叉树搜索树
106.从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
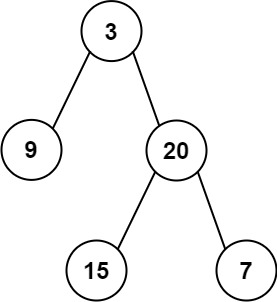
1
2
| 输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
|
示例 2:
1
2
| 输入:inorder = [-1], postorder = [-1]
输出:[-1]
|
实现思路
这道题的重点就在于如何切割后序和中序的数组,得到切割点我们都知道很容易,就是找打中序遍历中的后续的最后一个节点作为root节点,然后接下来就是切割, 然后给他的子孙节点赋值。
第一次我是使用拷贝数组 ,但是这样做的空间复杂度太高, 因为需要对数组进行拷贝操作。之后就是想出来的直接对参数进行数组的范围进行修改就可以避免这样的问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder.length == 0 || postorder.length ==0) return null;
int rootVal = postorder[postorder.length - 1];
TreeNode root = new TreeNode(rootVal);
int i =0;
for( ; i< inorder.length;i++){
if(inorder[i]== rootVal) break;
}
int lstart = 0;
int lend = i;
int[] newInorder = Arrays.copyOfRange(inorder, lstart,lend);
int[] newPostorder = Arrays.copyOfRange(postorder,lstart,lend);
root.left = buildTree(newInorder,newPostorder);
int inrstart = i + 1;
int inrend =inorder.length ;
int postrend = postorder.length -1;
int[] newInorder1 = Arrays.copyOfRange(inorder,inrstart, inrend);
int[] newPostorder1 = Arrays.copyOfRange(postorder,i, postrend);
root.right = buildTree(newInorder1, newPostorder1);
return root;
}
}
|
升级
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(postorder.length == 0 || inorder.length == 0)
return null;
return buildHelper(inorder, 0, inorder.length, postorder, 0, postorder.length);
}
private TreeNode buildHelper(int[] inorder, int inorderStart, int inorderEnd, int[] postorder, int postorderStart, int postorderEnd){
if(postorderStart == postorderEnd)
return null;
int rootVal = postorder[postorderEnd - 1];
TreeNode root = new TreeNode(rootVal);
int middleIndex;
for (middleIndex = inorderStart; middleIndex < inorderEnd; middleIndex++){
if(inorder[middleIndex] == rootVal)
break;
}
int leftInorderStart = inorderStart;
int leftInorderEnd = middleIndex;
int rightInorderStart = middleIndex + 1;
int rightInorderEnd = inorderEnd;
int leftPostorderStart = postorderStart;
int leftPostorderEnd = postorderStart + (middleIndex - inorderStart);
int rightPostorderStart = leftPostorderEnd;
int rightPostorderEnd = postorderEnd - 1;
root.left = buildHelper(inorder, leftInorderStart, leftInorderEnd, postorder, leftPostorderStart, leftPostorderEnd);
root.right = buildHelper(inorder, rightInorderStart, rightInorderEnd, postorder, rightPostorderStart, rightPostorderEnd);
return root;
}
}
|
105 从前序和中序遍历序列构造二叉树
思路和前序的一样, 只需要改变对应的边界条件即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder.length == 0 || inorder.length == 0) return null;
int rootVal = preorder[0];
TreeNode root = new TreeNode(rootVal);
int i=0;
for(;i < inorder.length;i++){
if(inorder[i] == rootVal) break;
}
int lstart = 0;
int lend = i;
int size = lend - lstart ;
int prelstart = 1;
root.left = buildTree(Arrays.copyOfRange(preorder,prelstart, prelstart + size),Arrays.copyOfRange(inorder,lstart,lend));
int rstart =i +1;
int rend = inorder.length;
root.right = buildTree(Arrays.copyOfRange(preorder,prelstart +size,preorder.length), Arrays.copyOfRange(inorder,rstart,rend));
return root;
}
}
|
二叉搜索树
对于二叉搜索树 用的最多的就是中序遍历,通过中序遍历得到的结果就是有序的。
还有一点就是在遍历二叉搜索树时最长用到的就是前缀指针, 通过前缀指针我们可以解决很多有关二叉搜索树属性的题型。
530.二叉搜索树的最小绝对差
给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。
示例:

提示:树中至少有 2 个节点。
实现思路
本题就是我们使用前缀节点的最好题型, 因为是二叉搜索树, 所以每两个相邻节点直接的差值才会出现最小的差值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
int res = Integer.MAX_VALUE;
TreeNode pre = new TreeNode(Integer.MIN_VALUE/2);
public int getMinimumDifference(TreeNode root) {
midorder(root);
return res;
}
public void midorder(TreeNode root){
if(root == null) return;
midorder(root.left);
res = Math.min(res,root.val - pre.val);
pre = root;
midorder(root.right);
}
}
|
501. 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
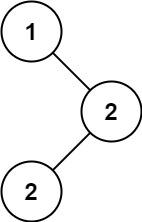
1
2
| 输入:root = [1,null,2,2]
输出:[2]
|
示例 2:
实现思路
本题中需要我们返回的不是一个众数, 而是一个数组,也就是说众数有很多个。
刚开始只有一个大概的思路,对于众数的数量统计不太明确以及相同众数的记录,没办法ac, 还是看了题解之后,才有明确的思路。
这道题也是使用前缀指针的一道典型题型,并且通过maxCount 和 count 两个变量来接收得到最大的众数。并且通过集合收集。
具体就是通过中序遍历, 如果遇到的节点的count大于maxCount ,那么就删除之前集合中存储的之前的众数。因为现在的这个节点的值最新的众数。如果遇到当前节点的count == maxCount, 那么就将当前节点入集合,他也是众数的一份子。
1
2
3
4
5
6
7
8
|
if (count > maxCount) {
res.clear();
res.add(root.val);
maxCount = count;
} else if (count == maxCount) {
res.add(root.val);
}
|
每次递归到当前节点都需要判断当前数值是需要加1 还是第一次遇到当前节点的值。
1
2
3
4
5
| if(pre == null || root.val != pre.val){
count = 1;
} else{
count++;
}
|
最后将集合中的数据全部转换为数组然后return。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
List<Integer> res = new ArrayList<>();
int maxCount =0;
int count = 0;
TreeNode pre = null;
public int[] findMode(TreeNode root) {
int count = 0;
find(root);
int[] resA = new int[res.size()];
for(int i=0 ;i< resA.length; i++){
resA[i] = res.get(i);
}
return resA;
}
public void find(TreeNode root){
if(root == null) return;
find(root.left);
if(pre == null || root.val != pre.val){
count = 1;
} else{
count++;
}
if (count > maxCount) {
res.clear();
res.add(root.val);
maxCount = count;
} else if (count == maxCount) {
res.add(root.val);
}
pre = root;
find(root.right);
}
}
|
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
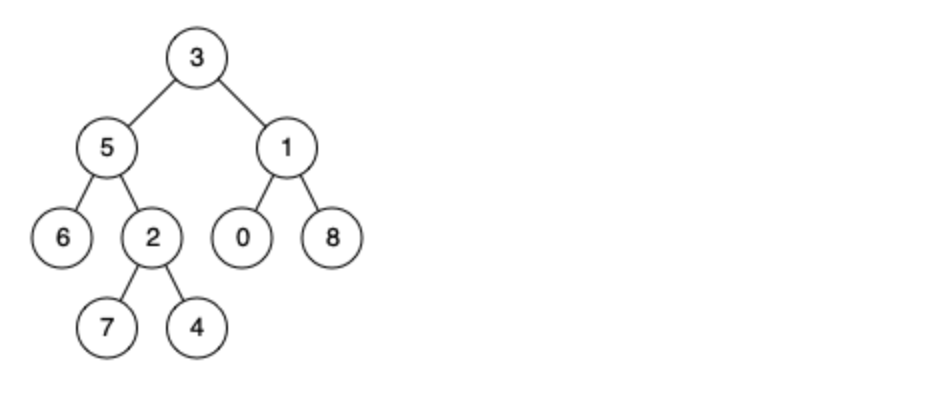
示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
实现思路
本题到现在我还是有点迷糊,不太明白为什么这样遍历得到的结果就是最近公共祖先。道行太浅…
所以思路暂时还是参考《代码随想录》代码随想录 (programmercarl.com)的内容吧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || q == root || p == root) return root;
TreeNode left = lowestCommonAncestor(root.left, p ,q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
System.out.print(root.val + "\t");
if(left != null && right != null) return root;
else if(left == null) return right;
else return left;
}
}
|
450.删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
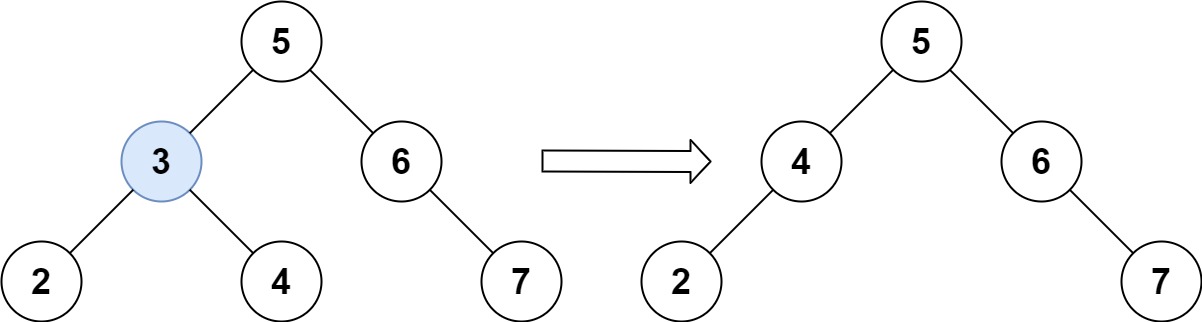
1
2
3
4
5
| 输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
|
示例 2:
1
2
3
| 输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
|
示例 3:
1
2
| 输入: root = [], key = 0
输出: []
|
实现思路
对于删除二叉树节点我们需要考虑的有个地方
- 删除的节点没有子节点
- 删除的节点有一个节点
- 要删除的节点有两个子节点
如果将这三种情况讨论清楚了, 那么这道题也就迎刃而解了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if(root == null) return root;
if(root.val == key){
if(root.left == null && root.right == null){
root = null;
return root;
}else if(root.left == null || root.right == null){
if(root.left == null){
root.val = root.right.val;
return root.right;
}else{
root.val = root.left.val;
return root.left;
}
}else{
TreeNode cur = root.right;
while(cur.left !=null){
cur = cur.left;
}
cur.left = root.left;
root = root.right;
return root;
}
}
if(root.val > key){
root.left = deleteNode(root.left, key);
}else if(root.val < key){
root.right = deleteNode(root.right, key);
}
return root;
}
}
|












