体系结构及内存分配
分层结构
- 内存
- cpu
- 外设
操作系统最核心的部分就是放在内核中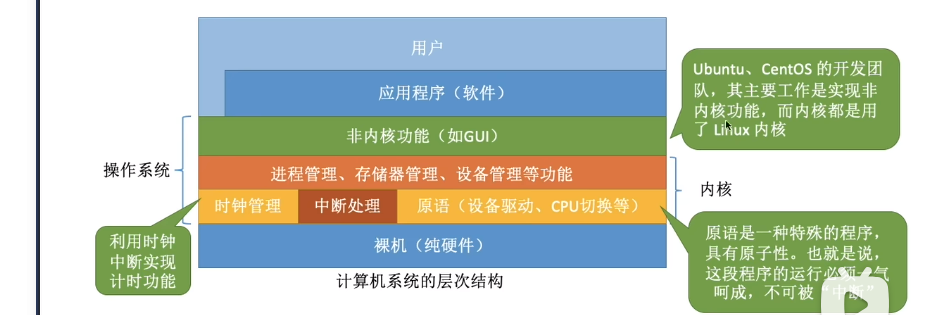
- 时钟管理
- 中断处理
- 原语 : 处于操作系统最底层, 与硬件直接接触
- 进程管理、存储器管理等
操作系统内核需要运行在内核态
非内核功能运行在用户态
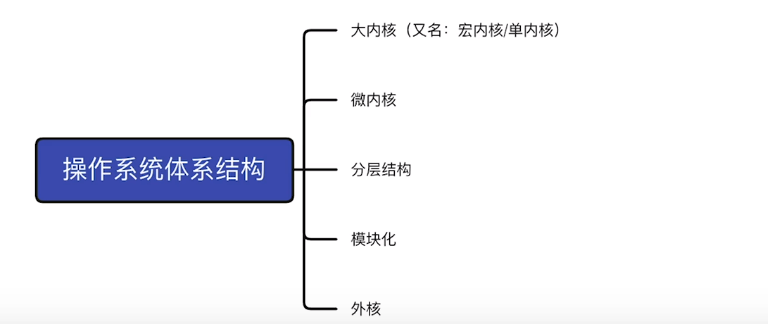
大内核
大内核的体系结构:
**所有的内核部分都是运行在内核态。 **
优缺点:
- 优点:
**高性能 **
- 缺点:
内核庞大, 结构混乱, 难以维持。
微内核
微内核的体系结果
对比大内核, 他只将
这些作为内核部分运行在内核态
优缺点:
- 优点:
内核功能少, 结构清晰, 方便维持。
- 缺点:
需要频繁的在用户态 和 内核态之间切换 ,性能低。
地址空间 & 地址生成
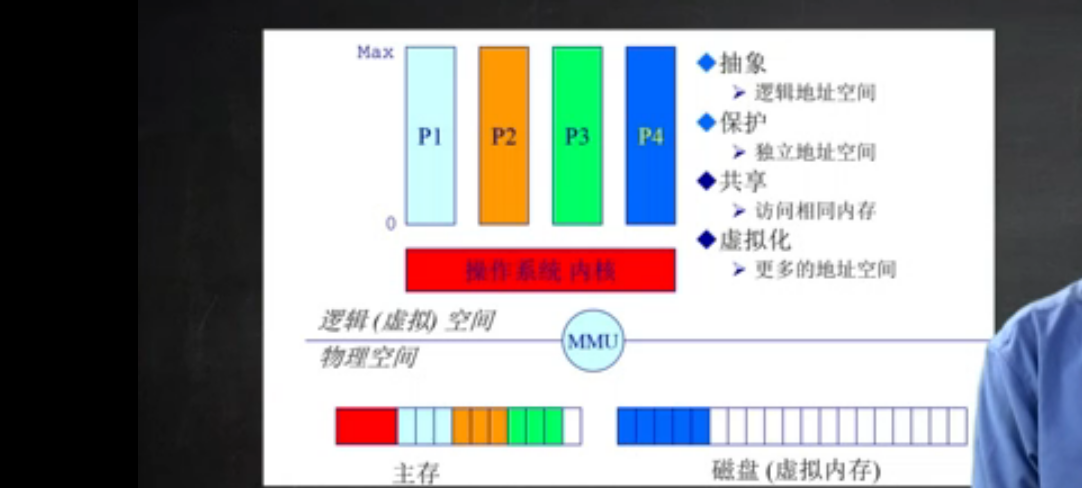
就上图而言, p1, p2 ,p3 ,p4 这四个进程在执行相对应的应用程序, 假设p1 先执行, p4 最后执行,那么我们就可以暂时将p4所需要的资源放到 磁盘中, 暂缓放到内存中 。而将真正需要内存的p1所需要的资源放到 内存中。
内存管理目标
- 抽象:逻辑地址空间
- 保护:独立地址空间
- 共享:访问相同内存
- 虚拟:更多的地址空间
内存管理方法
- 程序重定位
- 分段
- 分页
- 虚拟内存
- 按需分页虚拟内存
实现高度依赖于硬件, 其中**内存管理单元(MMU)**负责处理CPU的内存访问请求
地址空间的定义 & 生成
物理地址空间 : —–直接对应硬件支持的地址空间
逻辑地址空间: ——-一个运行的程序, 他所看到的空间(所拥有的内存范围),是一个一维的线性空间
两者的映射关系是由操作系统去协调
逻辑地址 是如何 对应到 物理地址的 ?
通过MMU表达了这种映射关系
- 当cpu要执行某个指令的时候 ,ALU部件(计算机组成原理中的内容)需要这条指令的内容。(也就是逻辑地址的内存内容)
- 内存管理单元(MMU)查询逻辑映射表 寻找在逻辑地址和物理地址之间的映射是否存在。
- 控制器通过总线向主存发送在物理地址的内存内容的请求
确保访问的内存地址合法
通过下面的步骤进行检查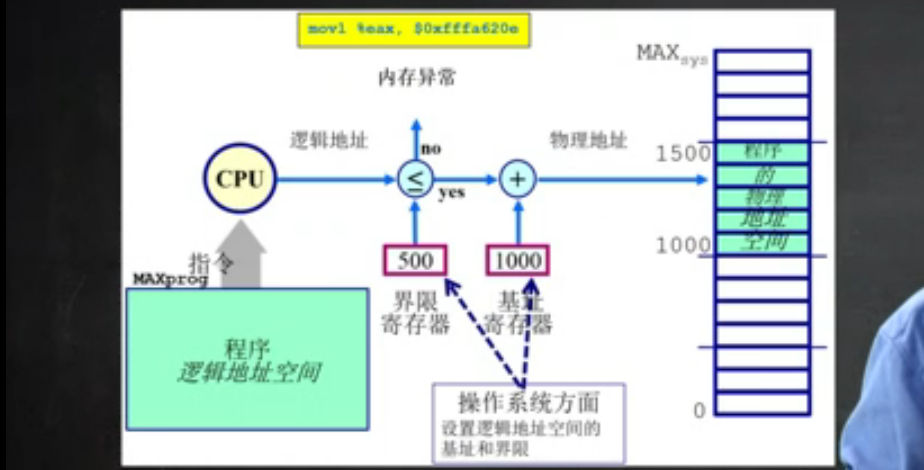
连续内存分配
内存的碎片问题
- 空闲内存不能被利用
- 外部碎片 ( 在分配单元之间的未使用内存)
- 内部碎片 ( 在分配单元中的未使用内存 )
分区的动态分配
**简单的内存管理方法: **
- 当应用程序准许运行时, 分配一个连续的区间
- 分配一个连续的内存区间给运行的程序以访问数据
分配策略
- 首次适配(第一匹配分配)
- 最优适配
- 最差适配
首次分配算法
按照地址顺序的空间块列表
分配需要寻找一个合适的分区
- 如果有, 那么就需要检查, 看是否自由分区能够合并于相邻的空闲分区
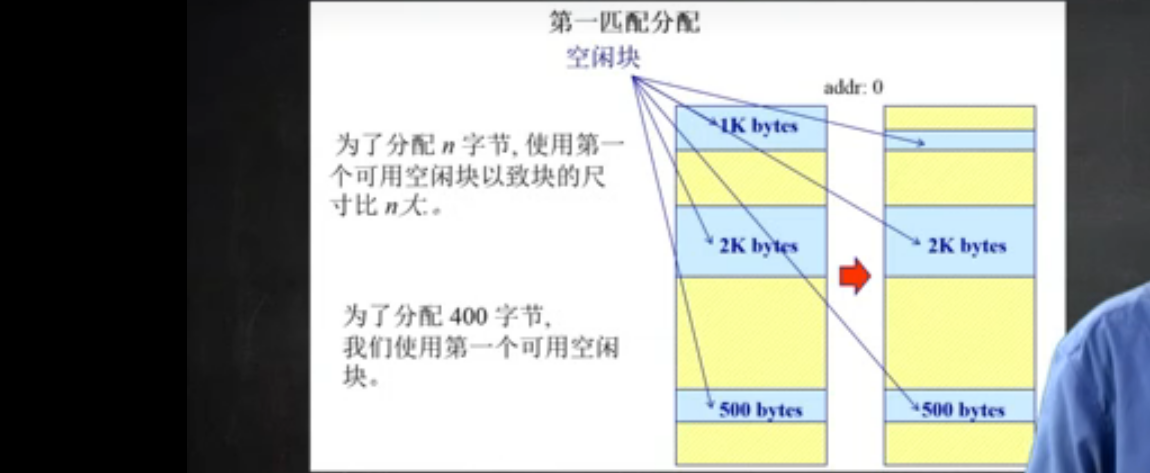
最优适配算法
** 在内存中找到最小的空闲块, 分配给应用程序**
- 为了避免分割大的空闲块
- 为了最小化外部碎片产生的尺寸
- 需求:
- 按照尺寸排序的空闲块列表
- 分配需要寻找一个合适的分区
- 重新分配需要搜索及合并于相邻的空闲分区
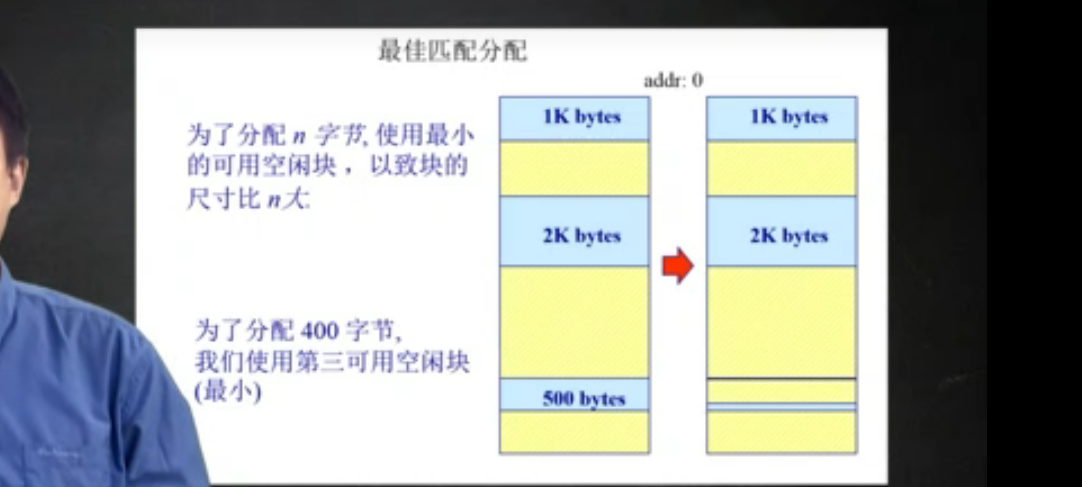
最差匹配算法
为了避免有太多微小的碎片
需求:
- 按尺寸排列的空闲块列表
- 分配很快(获得最大的分区)
- 重新分配需要合并于相邻的空闲分区, 如有, 需要调整空闲块列表
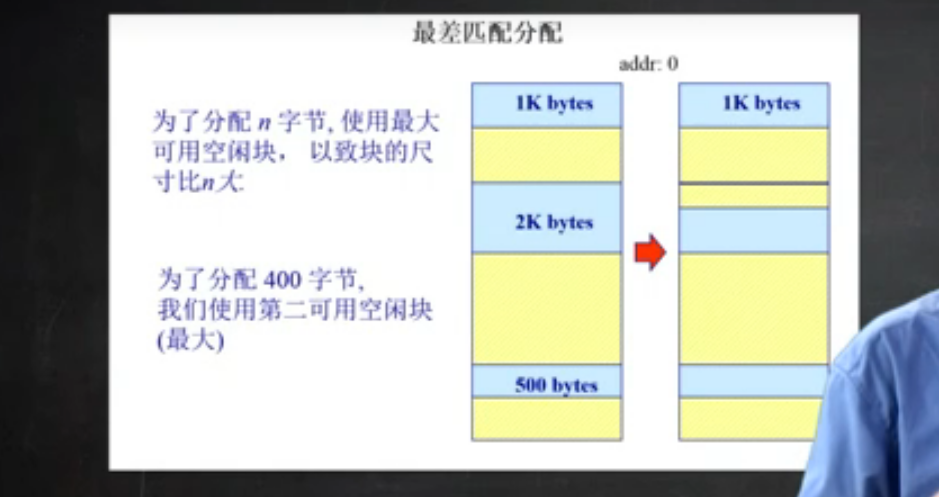
三种优缺点比较
| 分配方式 | 第一匹配分配 | 最优适配分配 | 最差适配分配 |
|---|---|---|---|
| 优势 | 简单 / 易于产生更大空闲块 | 比较简单 / 大部分分配是小尺寸时高效 | 分配很快 / 大部分分配是中尺寸时高效 |
| 劣势 | 产生外部碎片 / 不确定性 | 产生外部碎片 / 重分配慢 / 产生很多没用的微小碎片 | 产生外部碎片 / 重分配慢 / 易于破碎大的空闲块以致大分区无法被分配 |
压缩式碎片整理
- 压缩式碎片整理
- 重置程序以合并碎片
- 要求所有程序是动态可重置的
- 问题 :
- 何时重置 ? (在程序处于等待状态时才可以重置)
- 需要考虑内存拷贝的开销

交换式碎片整理
- 交换式碎片整理
- 运行程序需要更多的内存时,抢占等待的程序并且回收它们的内存
- 问题 :
- 哪些程序应该被回收 ?
- 情况 :运行中 : P3等待中 : P1 P2 P4内存分布 -> 主存 : OS / P1 / P3 / P2 / P4 磁盘 : 空当P3程序需要更大的内存时 ->内存分布 -> 主存 : OS / P1 / P3 / P2 磁盘 : P4
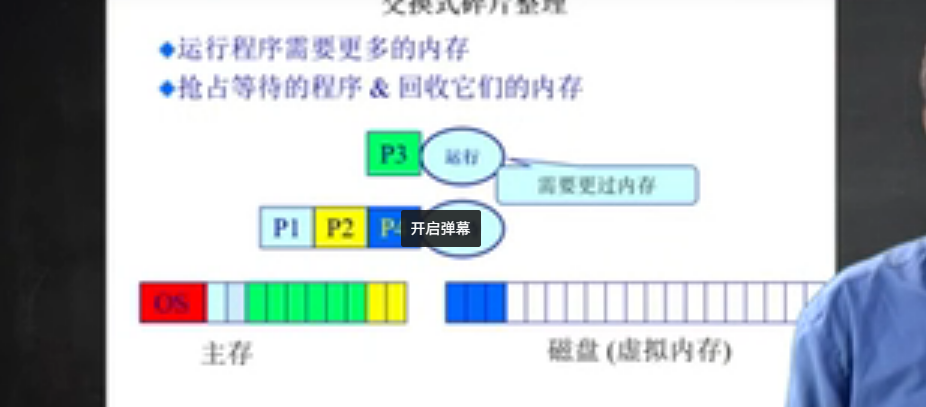
非连续内存分配
为什么要分连续内存分配管理方式 ?
答:连续分配的缺点就是会带来各种缺点, 内存利用率低, 外碎片、内碎片等问题。
随意** **
非连续分配的优点 :
- 一个程序的物理地址空间时非连续的
- 更好的内存利用和管理
- 允许共享代码与数据
- 支持动态加载和 动态链接
**非连续内存分配机制的缺点 : **
- 如果建立虚拟地址和物理地址之间的转换
- 软件方案
- 硬件方案
两种硬件方案:
- 分段机制
- 分页机制
分段机制
程序的分段地址空间
在程序中会有来自不同文件的函数 ; 在程序执行时, 不同的数据也有不同的字段, 比如 : 堆 / 栈 / .bss / .data 等
分段 : 更好的分离和共享
程序的分段地址空间如下图所示 :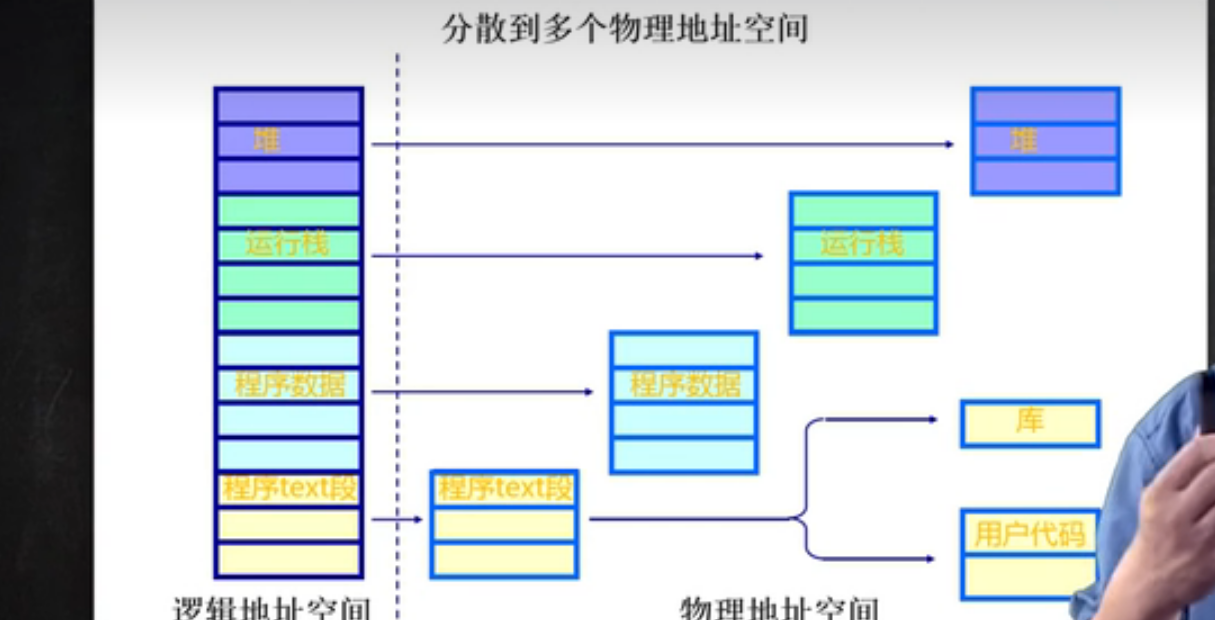
分段寻址方案
逻辑地址空间连续,但是物理地址空间不连续,使用映射机制进行关联.
一个段 : 一个内存”块”
程序访问内存地址需要 : 一个二维的二元组(s, addr) → (段号, 地址)
操作系统维护一张段表, 存储(段号, 物理地址中的起始地址, 长度限制)
物理地址 : 段表中的起始地址 + 二元组中的偏移地址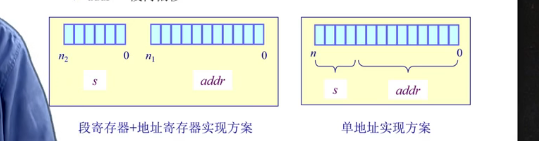
硬件实现方案:
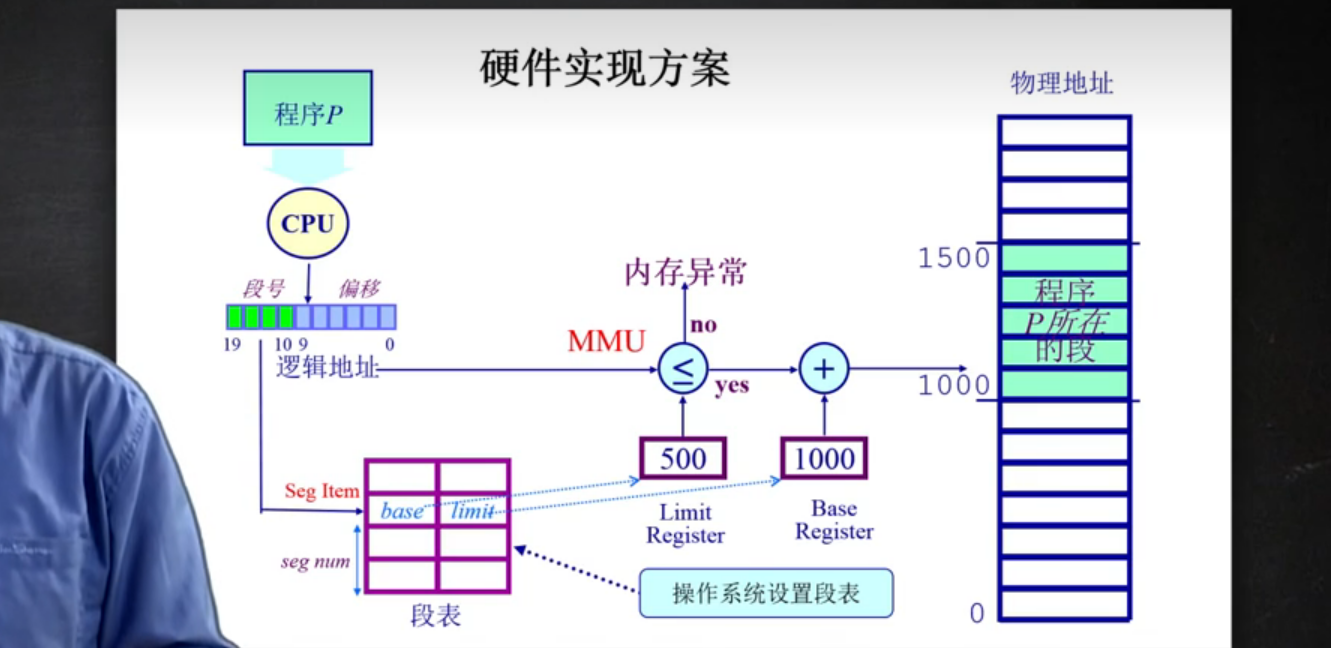
分页机制
分页地址空间
需要知道页号 + 页类的偏移
划分物理内存至固定大小的帧(Frame)
- 大小是2的幂, 512 / 4096 / 8192
划分逻辑地址空间至相同大小的页(Page)
- 大小是2的幂, 512 / 4096 / 8192
建立方案 → 转换逻辑地址为物理地址(pages to frames)
- 页表
- MMU / TLB
帧(Frame)
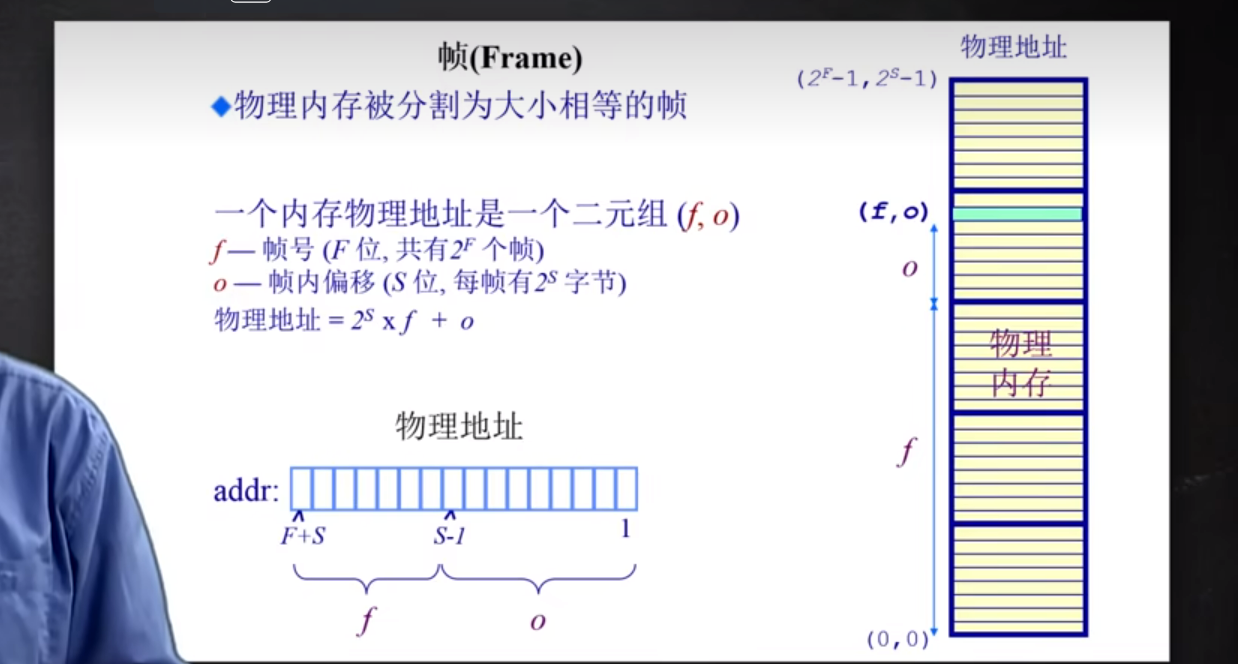
物理内存被分割为大小相等的帧. 一个内存物理地址是一个二元组(f, o) → (帧号, 帧内偏移)
帧号 : F位, 共有2^F个帧
帧内偏移 : S位, 每帧有2^S个字节
物理地址 = 2^S * f + o
(例子 : 16-bit地址空间, 9-bit(512 byte) 大小的页帧 物理地址 = (3,6) 物理地址 = 2^9 * 3 + 6 = 1542)
分页和分段的最大区别 : 这里的 S 是一个固定的数, 而分段中的长度限制不定
页(Page)
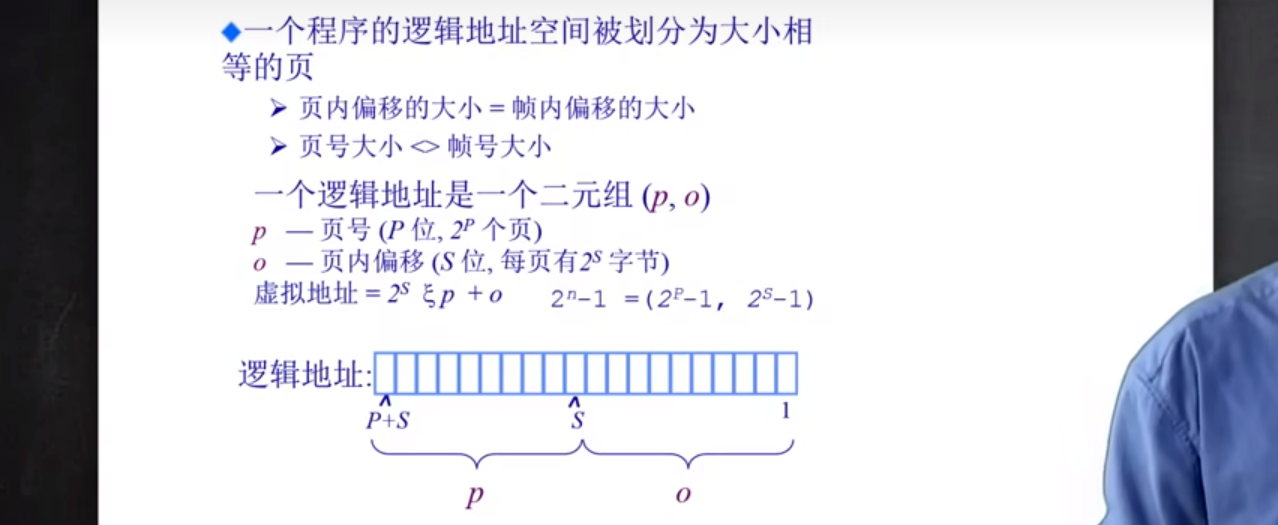
一个程序的逻辑地址空间被划分为大小相等的页. 页内偏移的大小 = 帧内偏移的大小 页号大小 <> 帧号大小
一个逻辑地址是一个二元组(p, o) → (页号, 页内偏移)
页号 : P位, 共有2^P个页
页内偏移 : S位, 每页有2^S个字节
虚拟地址 = 2^S * p + o
页的寻址机制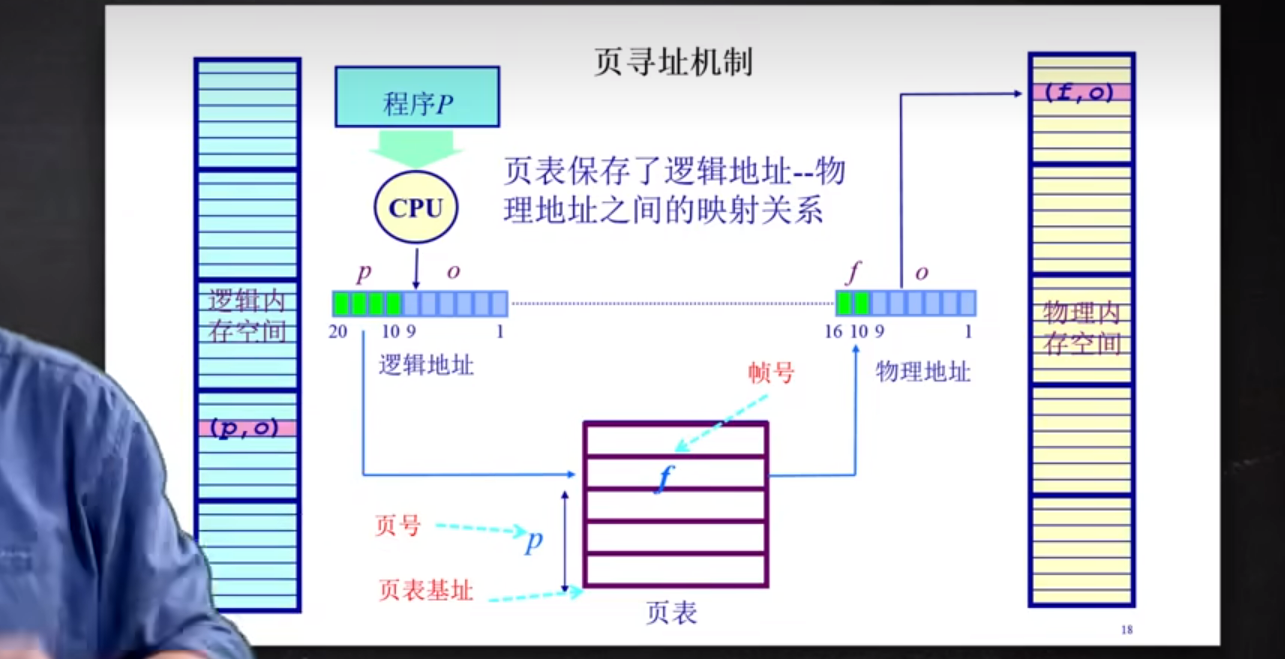
- 页映射到帧
- 页是连续的虚拟内存
- 帧是非连续的物理内存
- 不是所有的页都有对应的帧
分页机制的偏移大小是固定的。
页表
页表结构
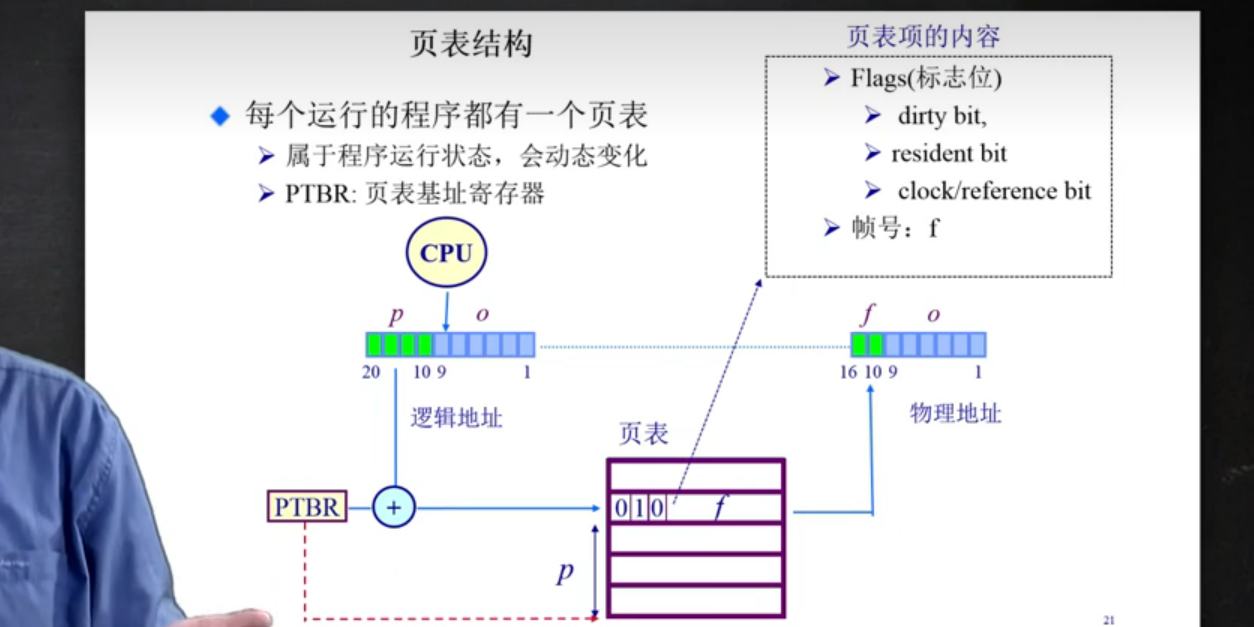
- 页表的概述
每一个运行的程序都有一个页表
- 属于程序运行状态, 会动态变化
- PTBR : 页表基址寄存器
- 转化后备缓冲区(TLB)
他是一块特殊的缓冲地。也可以说是cache。有效的解决了访问速度的问题。
也就是缓解时间问题
Translation Look-aside Buffer(TLB) 是一个缓冲区. CPU中有快表TLB(可以将经常访问的页表存放在这边)
缓存近期访问的页帧转换表项
- TLB使用关联内存实现, 具备快速访问性能
- 如果TLB命中, 物理页号可以很快被获取
- 如果TLB未命中, 对应的表项被更新到TLB中(x86的CPU由硬件实现, 其他的可能是由操作系统实现)
逻辑框图
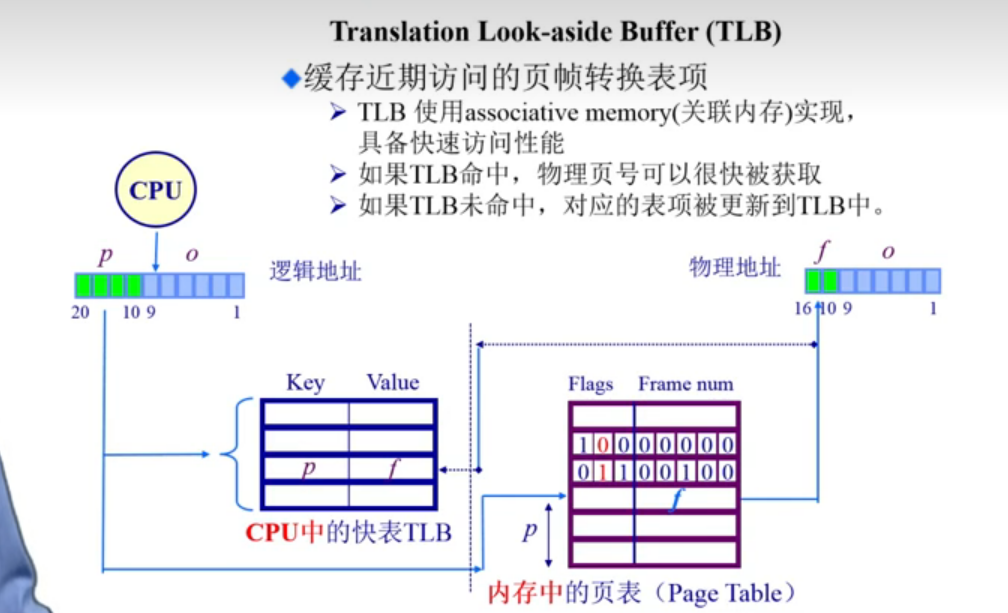
页表的缓冲流程
CPU根据程序的page的页号的若干位, 计算出索引值index, 在页表中搜索这个index, 得到的是帧号, 帧号和原本的offset组成物理地址.
- 二级/多级 页表
上述我们可以知道, 页表可以解决时间上的问题, 但是如何解决空间上的问题呢 ?
这里我们可以通过二级页表乃至多级页表来解决
也就是我们常说的时间换空间
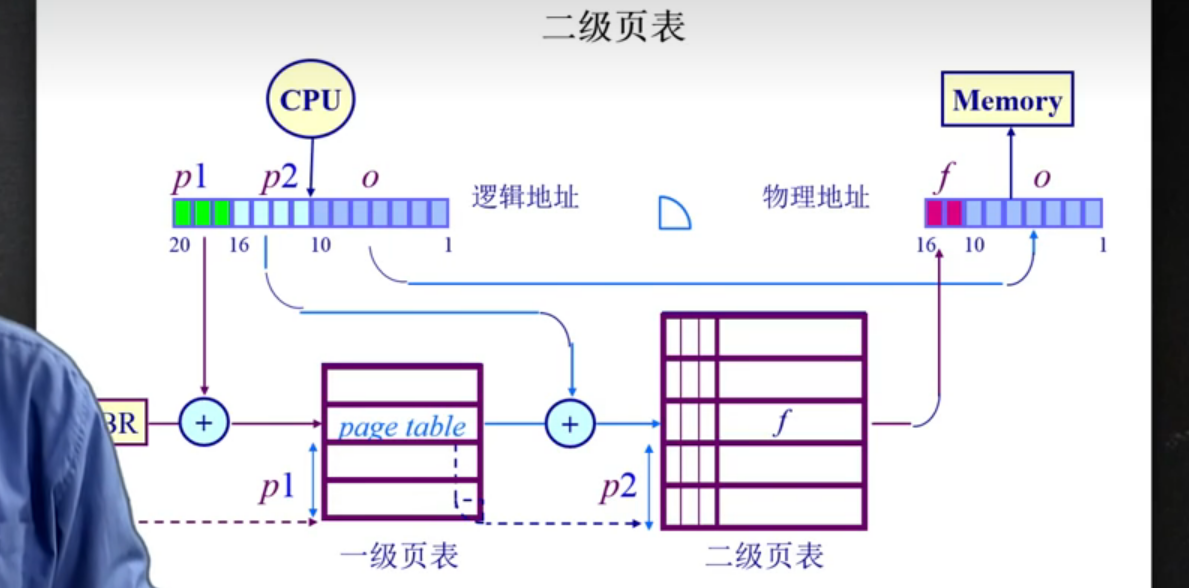
二级页表:
- 将页号分为两个部分, 页表分为两个, 一级页号对应一级页表, 二级页号对应二级页表.
- 一级页号查表获得在二级页表的起始地址, 地址加上二级页号的值, 在二级页表中获得帧号
- 节约了一定的空间, 在一级页表中如果resident bit = 0, 可以使得在二级页表中不存储相关index,而只有一张页表的话, 这一些index都需要保留
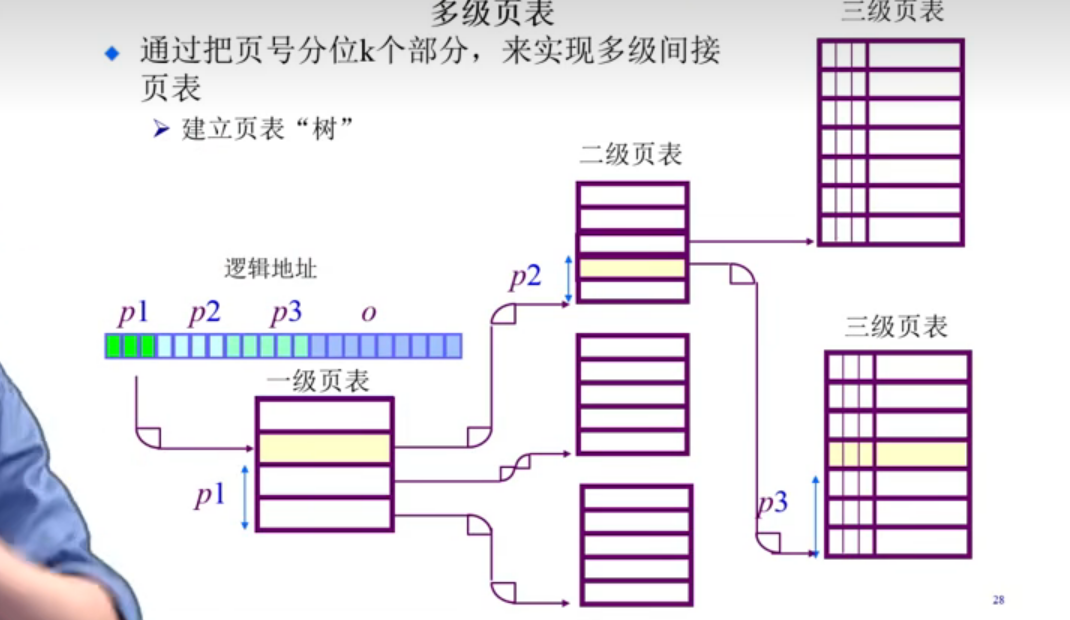
- 通过把页号分为k个部分, 来实现多级间接页表, 建立一棵页表”树”
- 反向页表
简单来说, 我们如果不知道物理地址空间大小, 那么就只能通过逻辑地址空间来建立, 这样就会浪费很多的空间。因为我们不知道实际的物理地址空间。
所以这里假设出了一种想法, 就是通过物理地址空间的大小来建立页表 。这样就可以避免了浪费。
方案一: : 基于页寄存器的方案
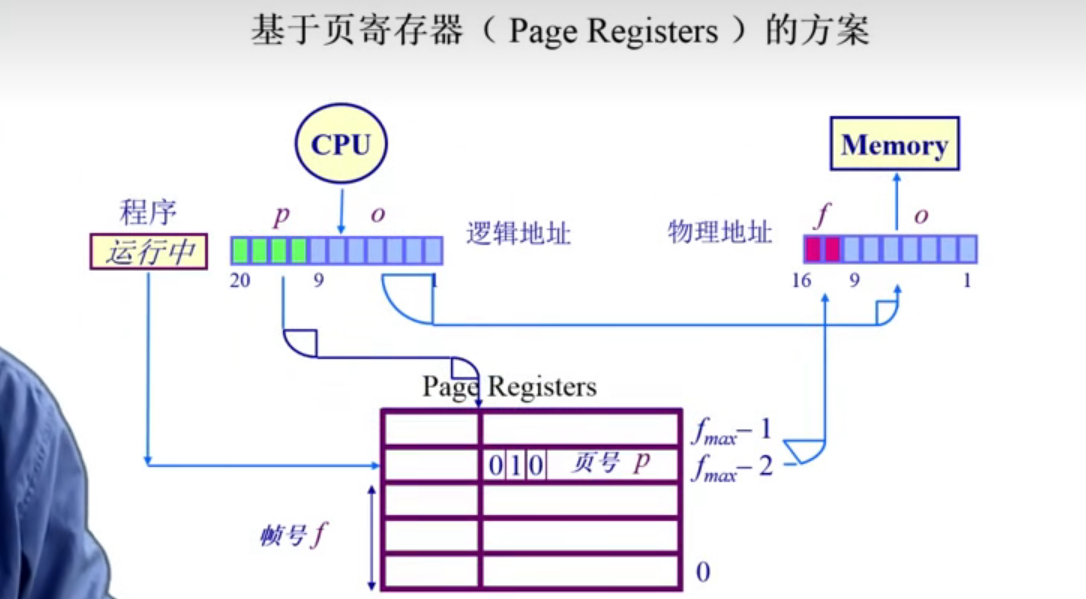
在页表中我们要解决的问题就是怎么通过页号 来找到页帧号
存储 (帧号, 页号) 使得表大小与物理内存大小相关, 而与逻辑内存关联减小.
每一个帧和一个寄存器关联, 寄存器内容包括 :
- resident bit : 此帧是否被占用
- occupier : 对应的页号 p
- protection bits : 保护位
实例 :
- 物理内存大小是 : 4096 * 4096 = 4K * 4KB = 16 MB
- 页面大小是 : 4096 bytes = 4 KB
- 页帧数 : 4096 = 4 K
- 页寄存器使用的空间(假设8 bytes / register) : 8 * 4096 = 32 Kbytes
- 页寄存器带来的额外开销 : 32K / 16M = 0.2%
- 虚拟内存大小 : 任意
优势 :
- 转换表的大小相对于物理内存来说很小
- 转换表的大小跟逻辑地址空间的大小无关
劣势 :
- 需要的信息对调了, 即根据帧号可以找到页号
- 如何转换回来? (如何根据页号找到帧号)
- 在需要在反向页表中搜索想要的页号
方案二 :基于关联内存的方案
硬件设计复杂, 容量不大, 需要放置在CPU中
如果帧数较少, 页寄存器可以被放置在关联内存中
在关联内存中查找逻辑页号
- 成功 : 帧号被提取
- 失败 : 页错误异常 (page fault)
限制因素:
- 大量的关联内存非常昂贵(难以在单个时钟周期内完成 ; 耗电)
所以这种一般不实用
方案三: 基于哈希(hash)的方案
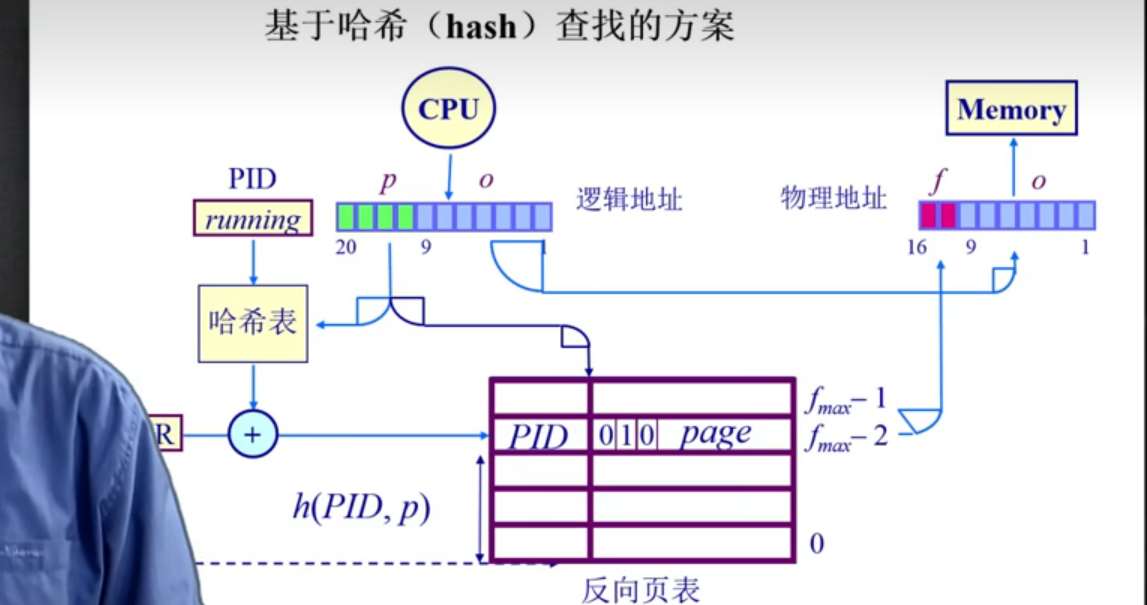
哈希函数 : h(PID, p) 从 PID 标号获得页号
在反向页表中通过哈希算法来搜索一个页对应的帧号
对页号做哈希计算, 为了在帧表中获取对应的帧号
页 i 被放置在表 f(i) 位置, 其中 f 是设定的哈希函数
为了查找页 i , 执行下列操作 :
- 计算哈希函数 f(i) 并且使用它作为页寄存器表的索引, 获取对应的页寄存器
- 检查寄存器标签是否包含 i, 如果包含, 则代表成功, 否则失败









