问题提出

首先，我们可以知道一个关系模式应当是五元组。

1
2
3
4
5
6
7
8
R(U,D,DOM,F)

- R : 就是关系名R是符号化的元组语义
- U : U为一组属性（也就是一个表中的属性集合）
- D : 为属性组U的属性所来自的域
- DOM : 为属性到域的映射
- F : 为属性组U上的一组数据依赖

因为D、DOM域模式设计关系不大， 因此我们这里暂不考虑

1
2
3
4
R<U,F>
当且仅将U上的一个关系r满足F时， r称为关系模式R<U,F> 的一个关系
	
	也就是说每一个属性都不能继续分割

作为一个二维表，关系要符合一个最基本的条件 ：

​ 每一个分量必须时不可分的数据项,满足这一条件的关系模式就属于第一范式

数据依赖:

​ 一个关系内部属性与属性之间的一种约束关系。

有许多数据依赖 ：最重要的就是函数依赖 和 多值依赖

1
2
3
4
5
6
7
格式 : 

Sname = f(Sno) ---也就是说Sno推出了Sname
记作:
Sno -> Sname
Sno -> Sdept
....

关系模式图：

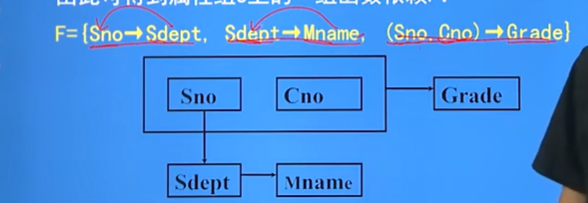
image-20230518121250329

该关系模式会出现的问题

  1. 数据冗余
  2. 更新异常
  3. 插入异常
  4. 删除异常

一个好的模式应当不会发生插入异常，删除异常，更新异常，数据冗余也要仅可能的少。

规范化

函数依赖

设R（U）是属性集U上的关系模式， X、Y是U的子集。（也就是说X、Y是Sno、Sname两个属性，U是这个属性组）

1
2
X函数确定Y 或者 说Y函数依赖于X
记作: X -> Y
  • 非平凡的函数依赖
1
X -> Y 但是y不属于x， 则称为X-> Y 是非平凡的函数依赖
  • 平凡的函数依赖
1
X -> Y  y属于x， 则称为X-> Y 是平凡的函数依赖
  • 完全函数依赖
1
2
3
4
在R（U）， 如果X-> Y ,并且对于x的任何一个真子集X`, 都有X` 不能推出 Y
则Y对X完全函数依赖 
记作:
X -F-> Y

也就说

（Sno, Cno）-->Grade : 想要得出Grade ,那么就必须知道Sno和Cno ， 缺一不可

  • 部分函数依赖
1
2
3
4
若X-> Y, 但是Y不完全依赖于X，则称Y对X部分函数依赖。
则Y对X完全函数依赖 
记作:
X -P-> Y

也就说

（Sno, Cno）-->Cno : 想要得出Cno ,那么只需要知道Sno和Cno 其中的一个即可

  • 传递函数依赖
1
2
3
在R（U）中，如果X->Y , Y-/->X, Y->Z, Z不属于Y，则成为Z对X传递函数依赖
记作:
X -传递-> Z

码

也就是我们平时所学的键, 只是叫法不同

1
设K为R<U,F>中得属性 或者属性组合， 若 K -F-> U，则K为R得候补码

包含在任何一个候补码中的属性被称为主属性， 反之，不包含在任何一个候补码中的属性被称为非主属性 / 非码属性。

最简单的情况下，单个属性是码， 最极端情况下，整个属性组都是码。称为全码

范式

范式也就相当于是规则。

关系型数据库中的关系要满足一定的要求， 满足不同程度的要求的为不同范式。

1
2
3
4
5
6
7
8
第一范式  : 1NF
依次类推
.....

-------
他们之间的关系是
5NF ∈ 4NF ∈ BCNF ∈ 3NF ∈ 2NF ∈ 1NF

2NF

若 R ∈ 1NF ，并且每个非主属性完全函数依赖于任何一个候选码， 则R ∈ 2NF .

比如 ： 

1
2
3
4
(Sno , Cno ) -F-> Grade # 非主属性 Grade 完全依赖于Sno 和 Cno
Sno -> Sdept , (Sno , Cno ) -P-> Sdept # 通过学号可以得出某个同学的住所， 而通过班级号也可以得到， 并不是完全函数依赖
（部分依赖）

如果说一个关系模型不满足 2NF,那么他就会出现以下几个问题 。

  1. 修改复杂
  2. 插入异常
  3. 删除异常

3NF

设关系模式 R<U,F> ∈1NF, 如不存在这样的码 X ，属性组 Y 及给主属性Z（Z !∈ Y ）使得 X-> Y,Y->Z成立。则称R<U,F> ∈3NF

1
2
简单来说。
X->Y ,Y->Z也就是传递函数依赖，不存在这个传递函数依赖。那么就成立3NF

BCNF

设关系模式 R<U,F> ∈1NF 若 X->Y 且 Y !∈ X时， X必含有码。则称R<U,F> ∈BCNF

重点 ： X必含有码

由上述BCNF的定义我们可以知道， 满足BCNF的关系依赖 。就必须要有

1
2
3
4
5
6
7
8
9
10
11
12
13
- 所有的非主属性对每个码都是完全函数依赖
- 所有主属性对每一个不包含他的码也是完全函数依赖
- 没有任何属性完全函数依赖于非码的任何一组属性


-----------------
举例: 
关系模型SJP(S, J, P)中， S是学生 ， J是课程 ，P 是名次。假设不存在相同排名的情况，每个同学的每个课程名次都是唯一的
那么就可以得到下面的函数依赖
(S, J) - > P  ; (J, P )-> S
作为候补码（s,p） and (j,p)两个码都是由两个属性构成， 他们是相交的 ，所以 SJP∈3NF.
同时除了码之外没有其他的决定因素 ，所以SJP ∈ BCNF

对于后续的多值依赖 与 4NF等等， 这里不做讲解。依次类推

**RANK()用法 : **

在数据库中，RANK() 是一个窗口函数，它为结果集中的每一行分配一个唯一的排名值。RANK() 函数根据指定的排序顺序对行进行排序，并为具有相同排序值的行分配相同的排名。在这种情况下，下一个排名值将是连续的整数序列中的下一个值。通常，RANK() 函数与 OVER() 子句一起使用，以指定排序依据的列。

以下是一个简单的例子，假设我们有一个名为 sales 的表，其中包含 salesperson 和 sales_amount 两个列。我们想要按销售额为销售人员排名：

1
2
3
SELECT salesperson, sales_amount,
       RANK() OVER (ORDER BY sales_amount DESC) AS rank
FROM sales;

在这个查询中，RANK() 函数根据 sales_amount 列的降序值为每个销售人员分配一个排名。OVER() 子句定义了排序依据的列。

如果你想根据分组为每个销售人员分配排名，可以使用 PARTITION BY 子句。例如，假设 sales 表还包含一个名为 region 的列，你可以按地区对销售人员进行排名：

1
2
3
SELECT region, salesperson, sales_amount,
       RANK() OVER (PARTITION BY region ORDER BY sales_amount DESC) AS rank
FROM sales;

在这个查询中，我们首先根据 region 列将销售人员分组，然后在每个分组内按 sales_amount 列的降序值为销售人员分配排名。PARTITION BY 子句允许我们在每个分组内重新开始排名。