图的定义
图是一种非线性数据结构, 由【顶点Vertex】 和 【边Edge】组成。我们可以将图G抽象地表示为一组顶点V 和一组边 E 地集合。
如下图就是图地网络关系 和 树 以及链表地区别
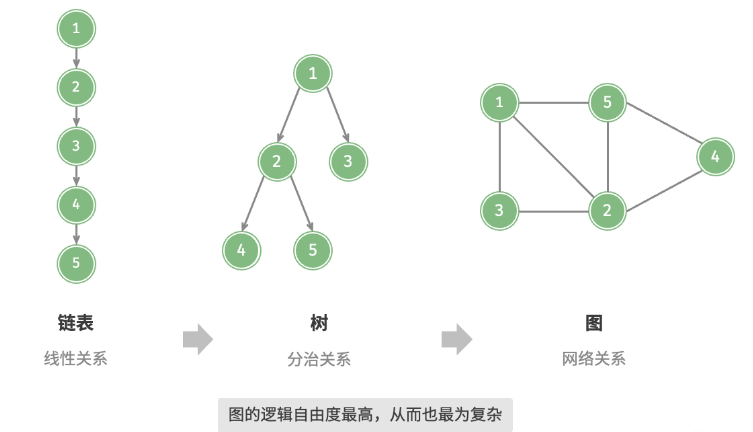
图与其他数据结构之间的关系我们可以抽象为
把顶点看作节点, 将边看作各个节点地指针。, 可以将图看作是一种从链表拓展而来的数据结构。它的复杂度 和 自由度更高。
图的常见类型
根据边是否具有方向,可分为「无向图 Undirected Graph」和「有向图 Directed Graph」
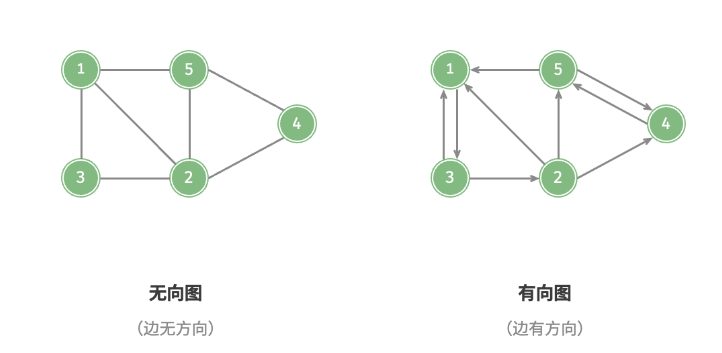
根据所有顶点是否联通,可分为「连通图 Connected Graph」和「非连通图 Disconnected Graph」
连通图 : 从一个顶点出发可以到达其余任意顶点。
非连通图 :从一个顶点出发 ,至少有一个顶点无法到达。
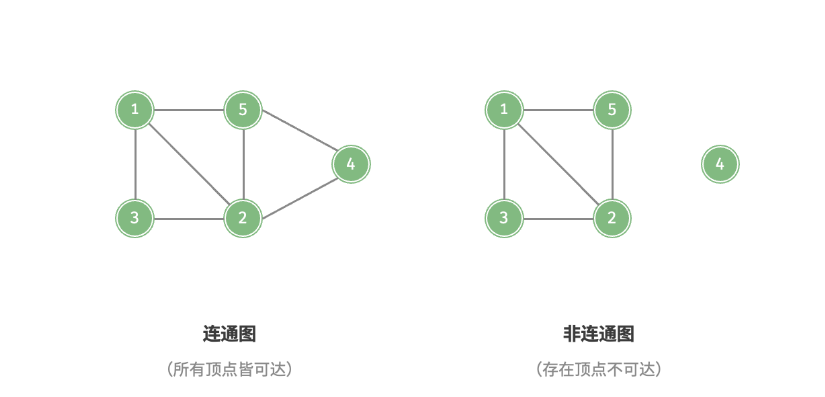
还可以为图添加权重变量, 从未得到有权图[Weighted Graph]
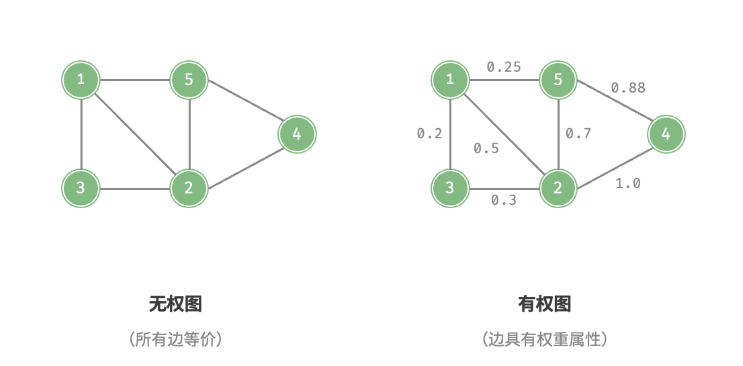
图的常用术语
图是由节点(vertices)和边(edges)组成的一种数据结构,常用术语包括:
- 有向图(Directed Graph):每条边都有一个方向,从一个节点指向另一个节点。
- 无向图(Undirected Graph):每条边没有方向,连接两个节点。
- 加权图(Weighted Graph):每条边都有一个权重值,表示两个节点之间的距离、代价等。
- 连通图(Connected Graph):图中的任意两个节点都可以通过路径相连。
- 子图(Subgraph):一个图的一部分,包含一些节点和它们之间的边。
- 点的度数(Degree):指与该节点相连的边的数目。
- 路径(Path):连接两个节点的一系列边构成的序列。
- 环(Cycle):路径的起点和终点相同的路径。
- 连通分量(Connected Component):无向图中的极大连通子图。
- 强连通分量(Strongly Connected Component):有向图中的极大强连通子图。
- 度(Degree): 表示一个顶点所拥有的边数,对于有向图, 那么描述变数就需要使用下面的两个出入度。
- 入度(In-degree):有向图中指向一个节点的边的数目。
- 出度(Out-degree):有向图中从一个节点出发的边的数目。
- 邻居(Neighbor)/邻接Adjacency:指与一个节点相连的其他节点。
- 序列(Sequence):一个节点序列,其中每个节点都与相邻的节点相连。
- 生成树(Spanning Tree):一个连通无向图的生成树是一个无环连通子图,包含所有节点,且仅有n-1条边。
图的表示方法
邻接矩阵:
设图的顶点数量为 n ,「邻接矩阵 Adjacency Matrix」使用一个 n×n 大小的矩阵来表示图,每一行(列)代表一个顶点,矩阵元素代表边,用 1 或 0 表示两个顶点之间是否存在边。
如下图所示,设邻接矩阵为 M 、顶点列表为 N ,那么矩阵元素M[i][j]=1 表示顶点 V[i]到顶点 V[j] 之间存在边,反之M[i][j]= 0 表示两顶点之间无边。
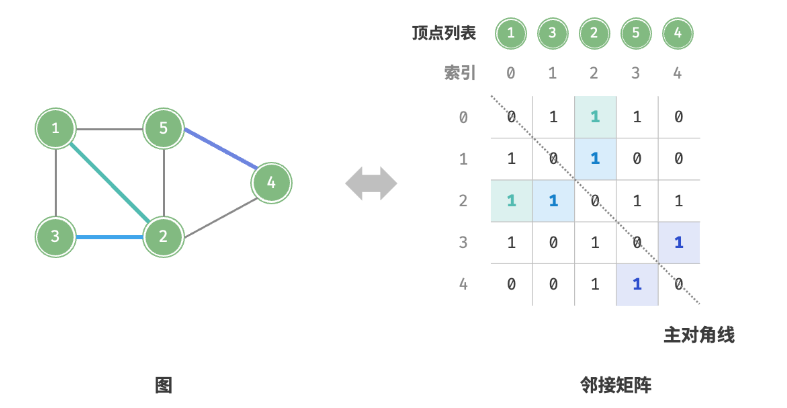
邻接表 :
使用邻接表法和 hash表有异曲同工之妙 。都是通过链表来实现。
「邻接表 Adjacency List」使用 n 个链表来表示图,链表节点表示顶点。第 i条链表对应顶点 i ,其中存储了该顶点的所有邻接顶点(即与该顶点相连的顶点)。
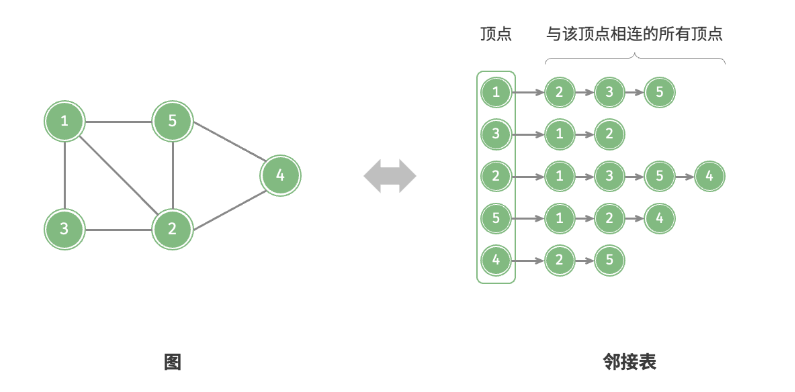
它相较于邻接矩阵最大的优点就是他存储的内容都是有用的, 而不是像邻接矩阵那样都存储。
同时,邻接表我们可以进行优化, 将链表过长的部分像hash表那样转换为红黑树。从而可以将时间效率从O(n)—-> O(log n)
基于邻接矩阵的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
| package tu;
import java.util.ArrayList;
import java.util.List;
public class GraphAdjMat {
List<List<Integer>> AdjMat;
List<Integer> vertices;
public GraphAdjMat(int[][] edges , int[] Vertices){
AdjMat = new ArrayList<>();
vertices = new ArrayList<>();
for (int i : Vertices){
addAdjMat(i);
}
for (int[] e : edges) {
addEdge(e[0], e[1]);
}
}
public void addAdjMat(int val){
int size = vertices.size();
vertices.add(val);
List<Integer> list = new ArrayList<>(size);
for (int i = 0; i < size; i++) {
list.add(0);
}
AdjMat.add(list);
for (List<Integer> row : AdjMat){
row.add(0);
}
}
public void addEdge(int m , int n){
if(m < 0 || n < 0 || m > vertices.size() || n > vertices.size() || m == n){
throw new IndexOutOfBoundsException("数组下标越界");
}
AdjMat.get(m).set(n,1);
AdjMat.get(n).set(m,1);
}
public void removeAdjMat(int m ,int n){
if(m < 0 || n < 0 || m > vertices.size() || n > vertices.size() || m == n){
throw new IndexOutOfBoundsException("数组下标越界");
}
AdjMat.get(m).set(n,0);
AdjMat.get(n).set(m,0);
}
public void removeVertices(int index){
if (index > vertices.size()){
throw new IndexOutOfBoundsException("数组下标越界, 无法删除");
}
vertices.remove(index);
AdjMat.remove(index);
for (List<Integer> row : AdjMat){
row.remove(index);
}
}
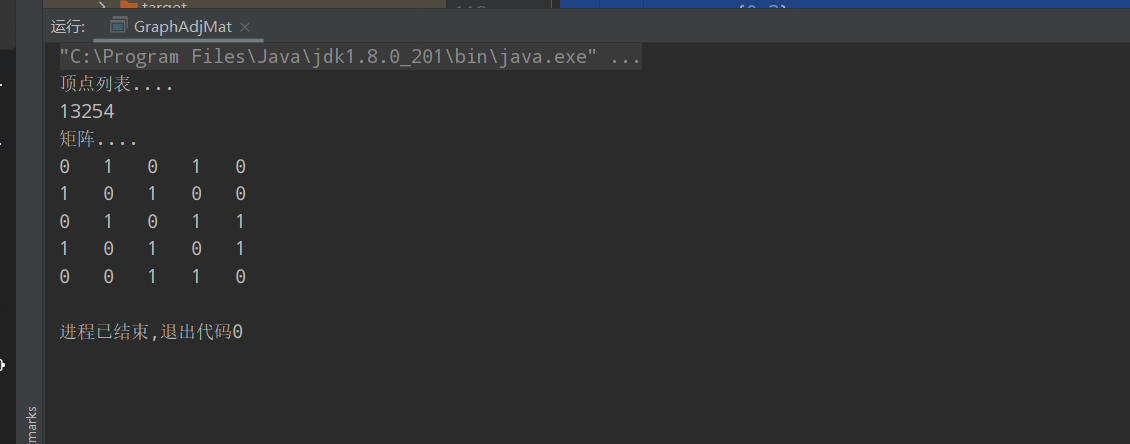
public void list(){
System.out.println("顶点列表....");
vertices.forEach(System.out::print);
System.out.println();
System.out.println("矩阵....");
for (int i = 0; i < AdjMat.size(); i++) {
for (int j = 0; j < AdjMat.get(i).size(); j++) {
System.out.print(AdjMat.get(i).get(j) + "\t");
}
System.out.println();
}
}
public static void main(String[] args) {
int[] vertices = new int[]{1,3,2,5,4};
int[][] edges = new int[][]{
{0,1},
{0,3},
{1,0},
{2,1},
{2,3},
{2,4},
{3,0},
{3,2},
{3,4},
{4,2},
{4,3}
};
GraphAdjMat graphAdjMat = new GraphAdjMat(edges,vertices);
graphAdjMat.list();
}
}
|
基于邻接表的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
| package tu;
import org.omg.CORBA.MARSHAL;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public class Graph {
Map<Vertex, List<Vertex>> adjList;
public Graph(Vertex[][] edges){
this.adjList = new HashMap<>();
for (Vertex[] edge : edges){
addVertex(edge[0]);
addVertex(edge[1]);
addAdjMat(edge[0],edge[1]);
}
}
private void addAdjMat(Vertex item0, Vertex item1) {
if (!adjList.containsKey(item0) || !adjList.containsKey(item1) || item0 == item1){
throw new IndexOutOfBoundsException("其中一个顶点不存在!");
}
if (!adjList.get(item0).contains(item1)){
adjList.get(item0).add(item1);
}
if (!adjList.get(item1).contains(item0)){
adjList.get(item1).add(item0);
}
}
private void addVertex(Vertex item) {
if(adjList.containsKey(item)){
return;
}
adjList.put(item,new ArrayList<>());
}
public void removeVertex(Vertex val){
if(!adjList.containsKey(val)){
throw new IndexOutOfBoundsException("顶点不存在");
}
adjList.remove(val);
for (Map.Entry<Vertex,List<Vertex>> item : adjList.entrySet()){
item.getValue().remove(val);
}
}
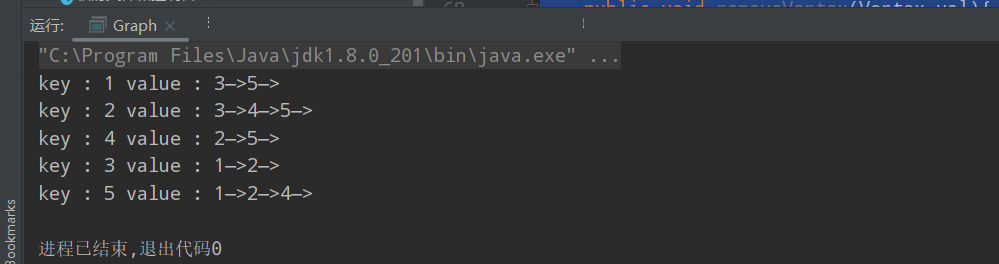
public void list(){
for (Map.Entry<Vertex,List<Vertex>> item : adjList.entrySet()){
System.out.print("key : " + item.getKey() + " value : ");
List<Vertex> value = item.getValue();
for (Vertex vertex : value){
System.out.print(vertex + "—>");
}
System.out.println();
}
}
public static void main(String[] args) {
Vertex vertex1 = new Vertex(1);
Vertex vertex3 = new Vertex(3);
Vertex vertex2 = new Vertex(2);
Vertex vertex5 = new Vertex(5);
Vertex vertex4 = new Vertex(4);
Vertex[][] vertices = new Vertex[][]{
{vertex1,vertex3},
{vertex3,vertex1},
{vertex2,vertex3},
{vertex5,vertex1},
{vertex4,vertex2},
};
Graph graph = new Graph(vertices);
graph.addAdjMat(vertex1, vertex5);
graph.addAdjMat(vertex3, vertex2);
graph.addAdjMat(vertex2, vertex5);
graph.addAdjMat(vertex2, vertex4);
graph.addAdjMat(vertex5, vertex2);
graph.addAdjMat(vertex5, vertex4);
graph.addAdjMat(vertex4, vertex5);
graph.list();
}
}
|
两者效率比较:
设图中共有 m 个顶点和 n 条边,下表为邻接矩阵和邻接表的时间和空间效率对比。
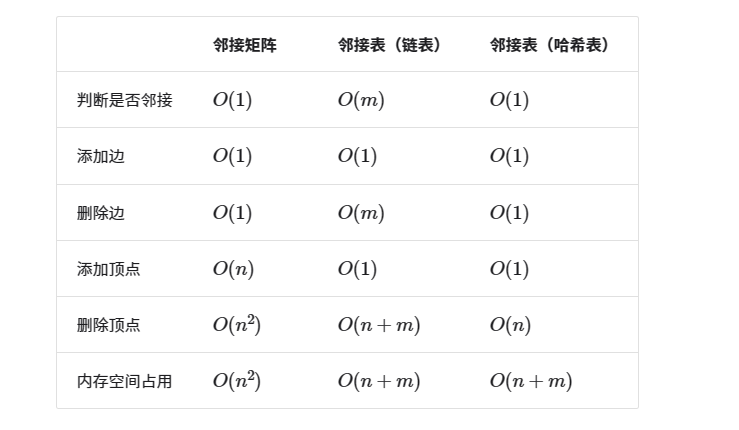
观察上表,似乎邻接表(哈希表)的时间与空间效率最优。但实际上,在邻接矩阵中操作边的效率更高,只需要一次数组访问或赋值操作即可。综合来看,邻接矩阵体现了“以空间换时间”的原则,而邻接表体现了“以时间换空间”的原则。














