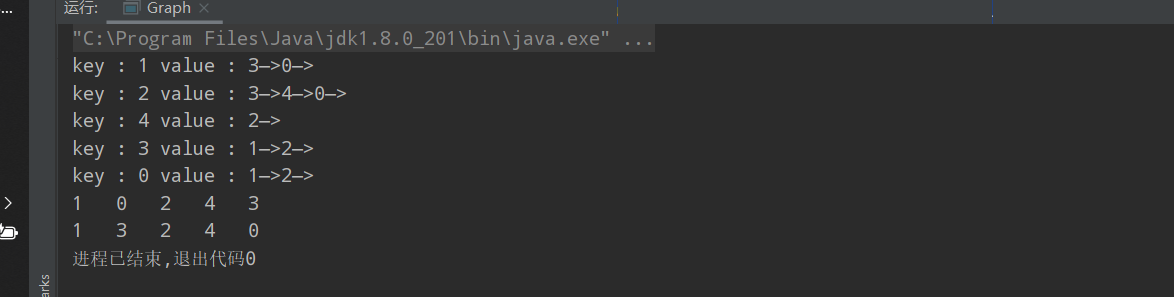
两种实现都是基于邻接表

DFS(深度优先搜索)

深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。具体地，从某个顶点出发，访问当前顶点的某个邻接顶点，直到走到尽头时返回，再继续走到尽头并返回，以此类推，直至所有顶点遍历完成。

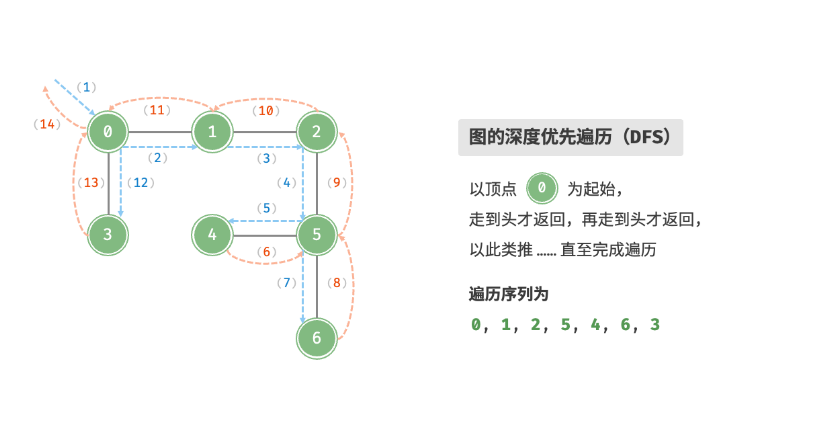
image-20230425185250331

这种算法一般我们可以用递归实现 ，也可以用栈实现。同样的， 我们需要接著一个辅助数组来记录我们已经访问过的顶点。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
public class Graph {
    // 邻接表，key: 顶点，value：该顶点的所有邻接顶点
    Map<Vertex, List<Vertex>> adjList;

    /**
     * 初始化邻接表
     * @param edges 两顶点之间的边的关系， edges中的数代表顶点上的数
     */
    public Graph(Vertex[][] edges){
        this.adjList = new HashMap<>();
        //添加顶点
        for (Vertex[] edge  : edges){
            addVertex(edge[0]);
            addVertex(edge[1]);
            //添加边
            addAdjMat(edge[0],edge[1]);
        }
    }

    /**
     * 添加两个顶点之间的关系， 也就是添加边的关系
     * @param item0 顶点0
     * @param item1 顶点1
     */
    private void addAdjMat(Vertex item0, Vertex item1) {
        //首先判断两个顶点是否存在， 如果不存在就不能添加边的关系
        if (!adjList.containsKey(item0) || !adjList.containsKey(item1) || item0 == item1){
            throw new IndexOutOfBoundsException("其中一个顶点不存在！");
        }
        if (!adjList.get(item0).contains(item1)){
            adjList.get(item0).add(item1);
        }
           if (!adjList.get(item1).contains(item0)){
            adjList.get(item1).add(item0);
        }

    }

    /**
     * 添加点 ，并且需要将扩展顶点
     * @param item 顶点val
     */
    private void addVertex(Vertex item) {
        //先判断顶点是否存在
        if(adjList.containsKey(item)){
            return;
        }
        adjList.put(item,new ArrayList<>());
    }

    /**
     * 删除顶点 ，同时需要删除所有有关它的边的关系
     * @param val 顶点的所有边的关系
     */
    public void removeVertex(Vertex val){
        //先判断顶点是否存在
        if(!adjList.containsKey(val)){
            throw new IndexOutOfBoundsException("顶点不存在");
        }
        adjList.remove(val);
        //先遍历每个顶点，然后看他里面是否存在val顶点， 存在就删除
        for (Map.Entry<Vertex,List<Vertex>> item : adjList.entrySet()){
           item.getValue().remove(val);
        }
    }

    //todo 打印邻接表
    public void list(){
        for (Map.Entry<Vertex,List<Vertex>> item : adjList.entrySet()){
            System.out.print("key : " + item.getKey() + " value : ");
            List<Vertex> value = item.getValue();
            for (Vertex vertex  : value){
                System.out.print(vertex + "—>");
            }
            System.out.println();

        }
    }
    /**
     * 深度优先搜索
     * @param adjList 存储元素的邻接表
     * @param vertex 传入遍历的节点
     * @param visited 记录当前节点地日志数组
     */
       public static void DFS(Map<Vertex, List<Vertex>> adjList,Vertex vertex,int[] visited){
        visited[vertex.val] = 1;
        System.out.print(vertex + "\t");
        List<Vertex> vertices = adjList.get(vertex);
        Iterator<Vertex> iterator = vertices.iterator();
        while(iterator.hasNext()){
            Vertex v = iterator.next();
            if(visited[v.val] == 0){
                DFS(adjList,v,visited);
            }
        }

    }


    public static void main(String[] args) {
        Vertex vertex1 = new Vertex(1);
        Vertex vertex3 = new Vertex(3);
        Vertex vertex2 = new Vertex(2);
        Vertex vertex5 = new Vertex(0);
        Vertex vertex4 = new Vertex(4);
        Vertex[][] vertices = new Vertex[][]{
                {vertex1,vertex3},
                {vertex3,vertex1},
                {vertex2,vertex3},
                {vertex5,vertex1},
                {vertex4,vertex2},
        };
        Graph graph = new Graph(vertices);
        graph.addAdjMat(vertex1, vertex5);
        graph.addAdjMat(vertex3, vertex2);
        graph.addAdjMat(vertex2, vertex5);
        graph.addAdjMat(vertex2, vertex4);
        graph.addAdjMat(vertex5, vertex2);
        graph.addAdjMat(vertex5, vertex4);
        graph.addAdjMat(vertex4, vertex5);
        graph.list();
        BFS(graph.adjList,vertex1);
        System.out.println();
        DFS(graph.adjList,vertex1);
    }

}

BFS(广度优先搜索)

广度优先遍历是一种由近及远的遍历方式，从距离最近的顶点开始访问，并一层层向外扩张。具体来说，从某个顶点出发，先遍历该顶点的所有邻接顶点，然后遍历下一个顶点的所有邻接顶点，以此类推，直至所有顶点访问完毕。

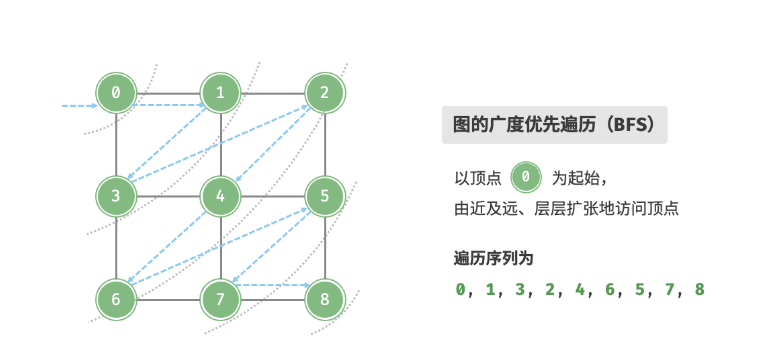
image-20230425190438910

广度优先搜索，我们使用的是队列来实现。先进先出 ，我们先将一个顶点加入队列， 然后当他出队列的时候，再将他身边的顶点加入队列。 ，循环往复，直到队列为空， 那么就是将所有的顶点遍历完成。

同时，我们这里也需要一个辅助数组， 用来记录已经加入队列遍历过的顶点。

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
package tu;

import org.omg.CORBA.MARSHAL;

import java.util.*;

/**
 * 基于邻接表实现图
 * 将顶点用顶点类Vertex 进行封装
 */
public class Graph {
    // 邻接表，key: 顶点，value：该顶点的所有邻接顶点
    Map<Vertex, List<Vertex>> adjList;

    /**
     * 初始化邻接表
     * @param edges 两顶点之间的边的关系， edges中的数代表顶点上的数
     */
    public Graph(Vertex[][] edges){
        this.adjList = new HashMap<>();
        //添加顶点
        for (Vertex[] edge  : edges){
            addVertex(edge[0]);
            addVertex(edge[1]);
            //添加边
            addAdjMat(edge[0],edge[1]);
        }
    }

    /**
     * 添加两个顶点之间的关系， 也就是添加边的关系
     * @param item0 顶点0
     * @param item1 顶点1
     */
    private void addAdjMat(Vertex item0, Vertex item1) {
        //首先判断两个顶点是否存在， 如果不存在就不能添加边的关系
        if (!adjList.containsKey(item0) || !adjList.containsKey(item1) || item0 == item1){
            throw new IndexOutOfBoundsException("其中一个顶点不存在！");
        }
        if (!adjList.get(item0).contains(item1)){
            adjList.get(item0).add(item1);
        }
           if (!adjList.get(item1).contains(item0)){
            adjList.get(item1).add(item0);
        }

    }

    /**
     * 添加点 ，并且需要将扩展顶点
     * @param item 顶点val
     */
    private void addVertex(Vertex item) {
        //先判断顶点是否存在
        if(adjList.containsKey(item)){
            return;
        }
        adjList.put(item,new ArrayList<>());
    }

    /**
     * 删除顶点 ，同时需要删除所有有关它的边的关系
     * @param val 顶点的所有边的关系
     */
    public void removeVertex(Vertex val){
        //先判断顶点是否存在
        if(!adjList.containsKey(val)){
            throw new IndexOutOfBoundsException("顶点不存在");
        }
        adjList.remove(val);
        //先遍历每个顶点，然后看他里面是否存在val顶点， 存在就删除
        for (Map.Entry<Vertex,List<Vertex>> item : adjList.entrySet()){
           item.getValue().remove(val);
        }
    }

    //todo 打印邻接表
    public void list(){
        for (Map.Entry<Vertex,List<Vertex>> item : adjList.entrySet()){
            System.out.print("key : " + item.getKey() + " value : ");
            List<Vertex> value = item.getValue();
            for (Vertex vertex  : value){
                System.out.print(vertex + "—>");
            }
            System.out.println();

        }
    }

    /**
     * 实现广度优先搜索 暂时规定
     * @param adjList 存储元素的邻接表
     * @param vertex 传入遍历的头节点
     */
    public static void BFS(Map<Vertex, List<Vertex>> adjList,Vertex vertex){
        Deque<Vertex> deque = new LinkedList<>();
        int size = adjList.size();

        int[] visited = new int[size];
        Arrays.fill(visited,0);
        //将入队列元素标记。 然后让元素入队列
        visited[vertex.val] = 1;
        deque.push(vertex);
        while (!deque.isEmpty()){
            Vertex poll = deque.poll();
            /*处理方法 */
            System.out.print(poll + "\t");
            List<Vertex> vertices = adjList.get(poll);
            for (Vertex v : vertices){
                if (visited[v.val] != 1){
                    deque.push(v);
                    visited[v.val] = 1;
                }
            }
        }

    }

    public static void main(String[] args) {
        Vertex vertex1 = new Vertex(1);
        Vertex vertex3 = new Vertex(3);
        Vertex vertex2 = new Vertex(2);
        Vertex vertex5 = new Vertex(0);
        Vertex vertex4 = new Vertex(4);
        Vertex[][] vertices = new Vertex[][]{
                {vertex1,vertex3},
                {vertex3,vertex1},
                {vertex2,vertex3},
                {vertex5,vertex1},
                {vertex4,vertex2},
        };
        Graph graph = new Graph(vertices);
        graph.addAdjMat(vertex1, vertex5);
        graph.addAdjMat(vertex3, vertex2);
        graph.addAdjMat(vertex2, vertex5);
        graph.addAdjMat(vertex2, vertex4);
        graph.addAdjMat(vertex5, vertex2);
        graph.addAdjMat(vertex5, vertex4);
        graph.addAdjMat(vertex4, vertex5);
        graph.list();
        BFS(graph.adjList,vertex1);
        System.out.println();
        DFS(graph.adjList,vertex1);
    }

}

运行结果

image-20230425113904576