排序实现

重新回顾实现十大排序算法

什么是排序， 就是元素按照关键字进行递减或者递增的顺序排列

**排序的稳定性： **

排序算法的稳定性是根据相同数值的元素之间的相对位置进行判断。

**内排序 and 外排序： **

所谓的内排序就是排序时不涉及数据的内、外存交换， 则成为内排序 ，反之涉及的话就是外排序。

​ 内排序适合元素个数不是很多的小表， 外排序适合多个表的数据进行排序。

​ 内排序是外排序的基础。

排序算法的性能 ：

排序算法的性能是根据时间 and 空间确定的

时间则是由元素比较和 移动的次数确定的

空间就是元素是否占用额外的存储空间

main函数

int main(){
    int nums[] = {12,21,11,0,8,53};
    int size = sizeof(nums)/ sizeof(int);
//    SelectSort(nums, size);
//    mopoSort(nums, size);
//    insertSort(nums,size);
    quickSort(nums,size);
    listNum(nums,size);
    return 0;

}

快速排序

/**
 * 快速排序  [是一种基于分治思想的排序算法]
 *      1. 选取数组最左端元素作为基准数，初始化两个指针 i 和 j 分别指向数组的两端；
        2. 设置一个循环，在每轮中使用 i（j）分别寻找第一个比基准数大（小）的元素，然后交换这两个元素；
        3. 循环执行步骤 2. ，直到 i 和 j 相遇时停止，最后将基准数交换至两个子数组的分界线；
 * @param nums 数组
 * @param size 大小
 */
void quickSort(int nums[] , int size){
    quick(nums, 0 , size - 1);
}

void quick(int *nums, int left , int right ){
    if (left >= right){
        return;
    }
    //进行划分
    int mid = partition(nums,left,right);
    //递归左右子数组
    quick(nums,left, mid);
    quick(nums, mid +1 ,right);
}


//进行划分
int partition(int nums[] , int left , int right){
    int i = left;
    int j = right;
    while(i < j){
        while(i < j && nums[j] >= nums[left]){
            j--;    //从右向左找小于基准数的数
        }
        while(i < j && nums[left] >= nums[i]){
            i++;    //从左向右找大于基准数的数
        }
        swap(nums,i,j);
    }
    swap(nums,i, left);
    return i;
}

void swap(int nums[], int left , int right){
    int temp = nums[left];
    nums[left] = nums[right];
    nums[right] = temp;
}

选择排序

/**
 * 选择排序
 *      实现思路
 *        首先进行遍历循环当前数组， 没遍历到一个数， 就以这个数为基数nums[i]。然后进行内层遍历[ i+1 -- size ]
 *        内层循环中就需要进行比较当前的数nums[j] 和 基数nums[i] 之间的大小关系
 *        找到本轮内层循环中的最小值， 放到最左边。
 *        依次往复，直到遍历到数组的最右端。
 * @param nums
 * @param size
 */
void SelectSort(int nums[], int size){
    /**
     * 在实现每轮排序的时候 ，将未排序部分的数中最小的放到数组的最左边
     */
     for(int i = 0 ; i <size; i++){
         int k  = i;
         //内排序部分，将每轮中最小的部分放到数组的开头
         for (int j = i + 1; j < size; j++) {
             if(nums[k] > nums[j]){
                 k = j;
             }
         }
         swap(nums[i],nums[k]);
     }

}

冒泡排序

/**
 * 实现冒泡排序
 * 从后向前进行遍历，以当前 nums[i] 为基数。 进行内循环从 [0 - i]
 * 如果说内层中有某个数nums[j] 比 基数 大， 那么就交换这个数nums[j]  和 基数 nums[i]
 * 如此往复 ，直到基数遍历到初始位置。
 * @param nums 数组
 * @param size 数组大小
 */
void mopoSort(int nums[] , int size){
    //先冒泡出来一个数字， 然后将其和其他的进行比较， 如果大于其那么就交换。然后知道
    for(int i = size -1 ;i > 0 ;i--){
        for (int j = 0; j < i; j++) {
            if (nums[i] < nums[j]){
                swap(nums[i],  nums[j]);
            }
        }
    }
}

插入排序

/**
 * 插入排序
 *      首先我们假设 基数之前的数已经排序好， 然后以后面的数为基数nums[i] 开始遍历之前的数，看看当前数插入的位置
 *      我们需要将前面的数一一记录 nums[j+1] = nums[j]
 *      直到[基数base < 遍历到的某个数nums[j]  或者 遍历到了最初位置 ]
 *      我们就需要将我们需要插入的基数 插入到当前的位置
 * @param nums 需要排序的数组
 * @param size 数组的大小
 */
void insertSort(int nums[] , int size){
    //需要用到递归
    for (int i = 1; i < size; i++) {
        int base = nums[i];
        int j = i - 1; // 从前一个已经排序好的数开始比较
        cout<<"当前的数为: "<<base <<endl;
        //如果说当前数nums[j] 小于 已经排好的数时，进行交换
        while( j >= 0 && nums[j] > base){
            nums[j+1] = nums[j];    //将当
            j--;
        }
        nums[j+1] = base;
        cout<<"排序后的顺序为: ";
        listNum(nums,size);
        cout <<endl;
    }
}

折半插入排序

/**
 * 折半插入排序
 * 折半插入排序相较于直接插入排序是在查找插入位置上做了优化。
 *      1. 首先根据索引找到需要插入的base元素
 *      2. base元素进行索引的区域 [ 0, i-1 ] ,因为插入排序的思想就是假设base元素之前的元素都是已经排序好的。
 *      3. 确定了插入的区域，我们就可以进行优化插入（进行折半）
 *          3.1.  通过while循环，先比较中间元素 和 base 元素的大小，
 *          3.2.  if(base >= nums[mid]) 就缩小查询的范围[ begin, end ] ---将begin改变---> [ mid+1 , end ]
 *          3.3.  if(base < nums[mid]) 就缩小查询的范围[ begin, end ] ---将end改变---> [ begin , mid - 1]
 *      4. 经过上述的操作， 我们就可以得到base的插入位置， 接下来就需要将数组中需要移动的元素整体向后移动。
 *      5. 然后插入到相应的位置。
 * @param nums 数组
 * @param size 数组大小
 */
void BinInsertSort(int nums[], int size){
    for (int i = 1; i < size; ++i) {
        int base = nums[i];
        int begin = 0;
        int end = i-1;
        //实现折半查找插入位置
        while(begin <= end){
            int mid = (begin + end) /2 ;
            if (nums[mid] >= base){
                end = mid - 1;
            }else {
                begin = mid + 1;
            }
        }
        //将元素整体向后移动一位， 给插入的元素腾出位置
        for (int j = i-1; j >= begin ; j--) {
            nums[j+1] = nums[j];
        }
        nums[begin] = base;
    }
}

归并排序

/**
 * 归并排序
 * 归并排序的思路还是分治思想的实现
 * 首先将元素通过递归的形式 分 ，分到最后两个元素就进行比较， 然后进行排序
 * 最后再通过回溯将排序好的元素进行插入
 * @param nums
 * @param size
 */
void mergeSort(int nums[], int size ){
    divide(nums, 0 , size- 1);
}



//进行递归的划分
void divide(int nums[] ,int left , int right){
    if(left >= right ){
        return;
    }
    int mid = (left + right) /2;
    divide(nums, left, mid);
    divide(nums, mid + 1, right);
    merge(nums, left, mid, right);
}



/**
 * 归并实现
 * todo 注意点: 边界取值问题
 * @param nums 需要排序的数组
 * @param left 数组左边index
 * @param mid 数组中间
 * @param right 数组右边index
 */
void merge(int nums[], int left, int mid, int right){
    int size= right - left + 1;
    int temp[size] ;
    //1.  先定义一个辅助数组， 将原数组的内容全部copy到辅助数组中
    int i = left, j = mid + 1; //左右数组的起始位置index
    int index = 0;
    while(i<= mid && j <= right ){
        //比较左右数组的元素大小， 将较小的那个加入到新数组中
        if (nums[i] < nums[j]){
            temp[index++] = nums[i++];
        }
        else{
            temp[index++] = nums[j++];
        }
    }
    //如果还有左数组 || 右数组 还有元素没有添加进入那就全部导入

    while( i <= mid){
        temp[index++] = nums[i++];
    }

    while( j <= right){
        temp[index++] = nums[j++];
    }

    //然后将临时数组中的元素全部转到原来的数组中

    // 将临时数组中的元素复制回原数组
    for (int p = 0; p < index; p++) {
        nums[left + p] = temp[p];
    }
}

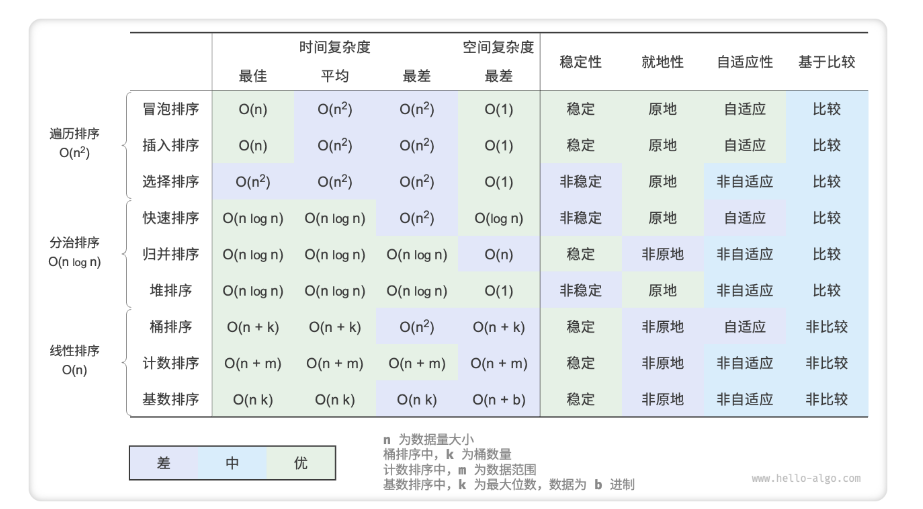
各排序的性能

参考： hello-算法

小结 - Hello 算法 (hello-algo.com)