回溯的适用范围

回溯法，一般可以解决如下几种问题：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等等

三大关键点

回溯法解决的问题都可以抽象为树形结构

**集合的大小就构成了树的宽度，递归的深度，都构成的树的深度**。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）

回溯模板就是递归三部曲

遇到题目的解法

首先，一定要分类是哪类题。组合、分割、子集还是棋盘…

组合

最经典的题目

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

在没有学习回溯之前我们可能就是只会n层for循环来解决这种题

在学习了回溯之后，我们就可以先进行画图分析【图片来自代码随想录: 连接代码随想录 (programmercarl.com)】

77.组合

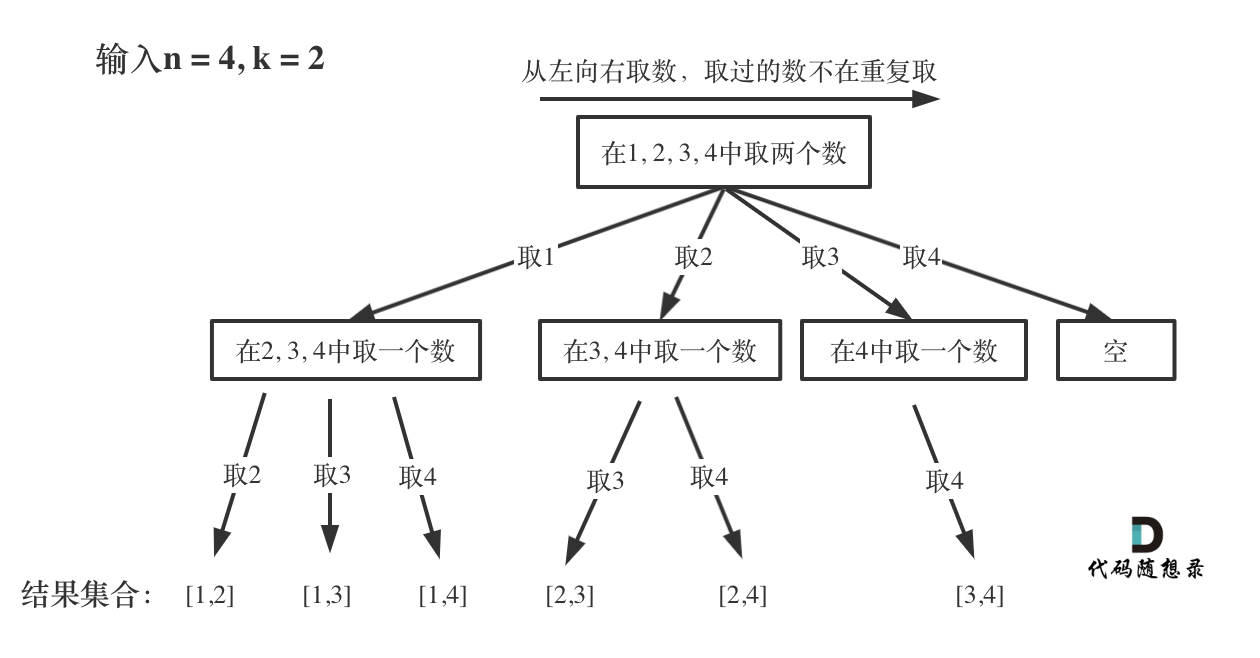
思路很显然就是递归三部曲

  • 递归返回值、参数
1
2
3
4
5
6
7
8
9
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
	//....
    combineHelper(....);
}

private void combineHelper(int n, int k, int startIndex){
}
  • 递归终止条件
1
2
3
4
5
 //终止条件
if (path.size() == k){
    result.add(new ArrayList<>(path));
    return;
}
  • 单层递归逻辑
1
2
3
4
5
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
    path.add(i);
    combineHelper(n, k, i + 1);
    path.removeLast();
}

对于这种类型的题思路我们需要很清晰

因为这道题他需要的是【1 … n 中所有可能的 k 个数的组合】那么其中的重点我们就可以get到

  1. 组合！！！
  2. 给出的元素不重复
  3. 需要的是k个数的组合
  4. 根据实例给出的答案可以得出【各个集合不重复】

由上述的get点，我们就可以是实现我们的思路了。

组合: 那么就是 使用回溯算法

给出的元素不重复: 不需要我们自己手动去重

得出的各个集合不重复: 需要使用index指针来移动递归的位置

组合Ⅱ

根据上一题的思路，我们再来看看这道题的解法

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

  • 所有数字都是正整数。
  • 解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

get关键点

  1. 组合
  2. 解集不能重复
  3. 给出的元素不重复
  4. 所有相加之和为 n 的 k 个数的组合

根据上面我们罗列的要求，我们就可以实现思路了。

组合: 那么就是 使用回溯算法

给出的元素不重复: 不需要我们自己手动去重

解集不能包含重复的组合: 使用index指针来移动递归的位置

题目中需要得是【和为n的k个数】

那么就需要将得出的数进行相加，如果和为 n 那么就将得出集合加入结果集中

此时我们传参就不能再向之前那样了

1
2
3
4
5
6
7
8
9
10
11
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();

public List<List<Integer>> combinationSum3(int k, int n) {
	backTracking(n, k, 1, 0);
	return result;
}
//递归函数
private void backTracking(int targetSum, int k, int index, int sum) {
   
   }

我们需要传入求和的参数sum，来对每一个得出的元素进行相加

1
2
3
4
5
6
7
8
9
10
//单层递归的逻辑
for(int i = index; i < k ;i++ ){
    sum += i;
    path.add(i);
    backTracking(targetSum,k, i + 1,sum);
    //回溯
    sum-=i;
    path.remove(path.size() - 1);
    
}

组合总和Ⅱ

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明： 所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

  • 示例 1:
  • 输入: candidates = [10,1,2,7,6,1,5], target = 8,
  • 所求解集为
1
2
3
4
5
6
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]
  • 示例 2:
  • 输入: candidates = [2,5,2,1,2], target = 5,
  • 所求解集为:
1
2
3
4
[
  [1,2,2],
  [5]
]

get关键点

  1. 组合
  2. 解集不能重复
  3. 给出的元素重复
  4. 所有数组中元素之和为 target的组合

重点

给出的元素重复

因为给出的元素重复，而我们的结果集中不能有重复的组合，那么我们单层递归的逻辑就需要发生一些改变

如图:【图片来自代码随想录: 代码随想录 (programmercarl.com)】

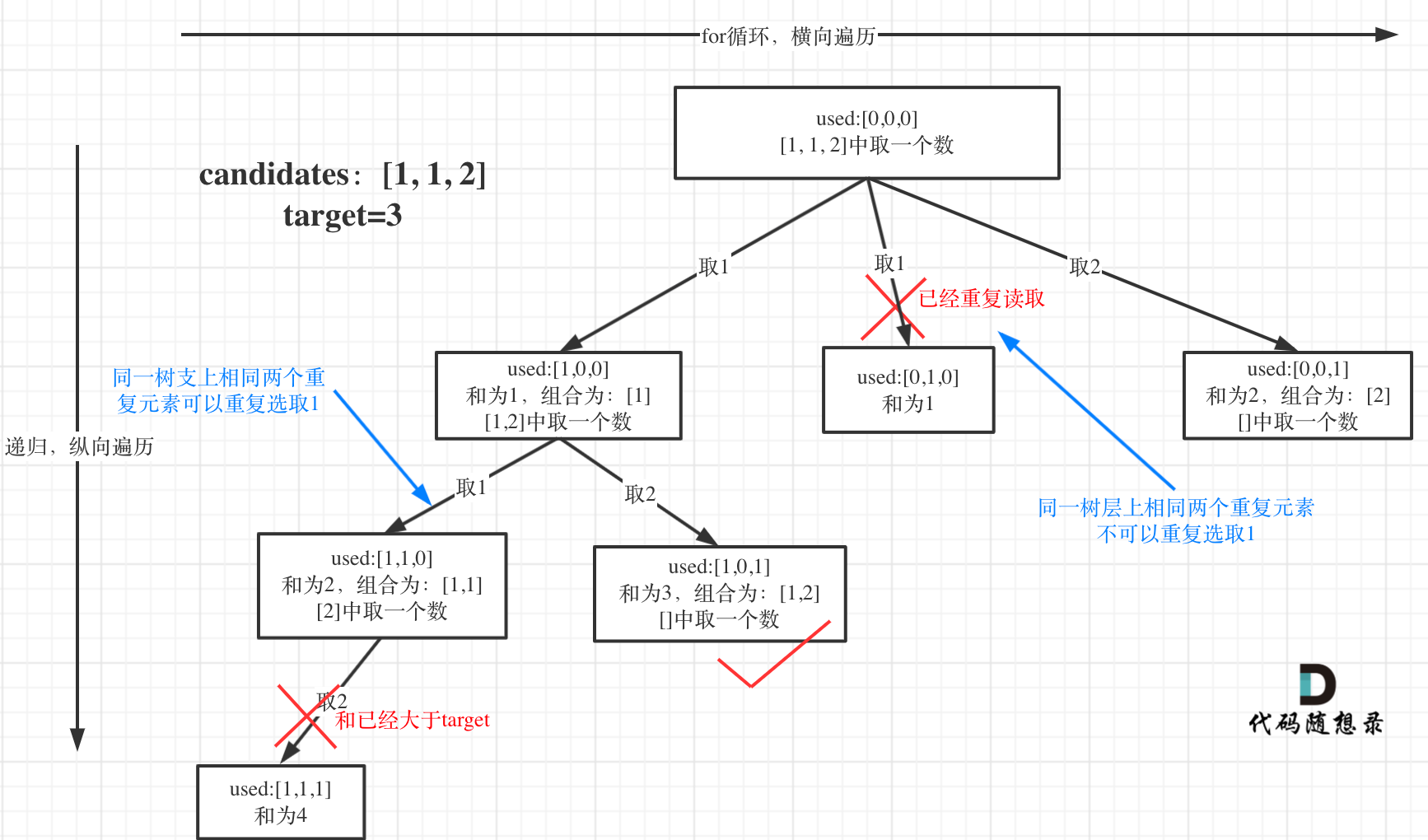
40.组合总和II

  1. 首先我们需要将题目中给出的数组进行排序，让相同的元素处于相邻的位置
  2. 借用used数组，对已经用过的数组中的元素进行标记
  3. 判断如果i > 0 && nums[i] == nums[i-1] && used == 0 ， 那么就可以说明相邻的数组是重复的，只需要跳过本次循环即可。
  4. 对于树枝循环，如果数组使用过了，那么就设置对应的used[i] == 1; 当一个树枝走到头 ，也就是到达叶子节点。那么就进行回溯，将used数组中设置的1清 0 。调用下一个树枝时重新进行设置used = 1 。进入③再次进行判断
  5. 直到index指向数组的最后一个元素。那么递归就结束了

对应的实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> ans = new ArrayList<>();
    //2. 借用used数组，对已经用过的数组中的元素进行标记
    int[] used;
    int sum = 0;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        used = new int[candidates.length];
        // 1. 为了将重复的数字都放到一起，所以先进行排序
        Arrays.sort(candidates);
        backTracking(candidates, target, 0);
        return ans;
    }

    private void backTracking(int[] candidates, int target, int startIndex) {
        if (sum == target) {
            ans.add(new ArrayList(path));
        }
        for (int i = startIndex; i < candidates.length; i++) {
            //对于大于target的元素不进行递归，降低时间复杂度
            if (sum + candidates[i] > target) {
                break;
            }
            //3.  出现重复节点，同层的第一个节点已经被访问过，所以直接跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0) {
                continue;
            }
            //4. 对于树枝上使用过的元素进行赋值为 1
            used[i] = 1;
            sum += candidates[i];
            path.add(candidates[i]);
            // 5. 每个节点仅能选择一次，所以从下一位开始
            backTracking(candidates, target, i + 1);
            used[i] = 0;
            sum -= candidates[i];
            path.remove(path.size() - 1);
        }
    }
}

切割字符串

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: “aab” 输出: [ [“aa”,”b”], [“a”,”a”,”b”] ]

get关键点

  1. 分割成一些字符串
  2. 每个字符串都是回文串

根据上面的要求，我们首先能确定的是这道题用回溯算法做

那么就可以将这道题抽象成为一个树结构

如图:【图片来自代码随想录: 代码随想录 (programmercarl.com)】

131.分割回文串

其次，我们需要判断我们切割的字符字串是不是回文串

判断我们就可以封装成为一个函数

1
2
3
4
5
6
7
8
9
 //判断是否是回文串
private boolean isPalindrome(String s, int startIndex, int end) {
    for (int i = startIndex, j = end; i < j; i++, j--) {
        if (s.charAt(i) != s.charAt(j)) {
            return false;
        }
    }
    return true;
}

对于切割字符串，因为我们已经确定这道题使用回溯算法做，那么就可以用递归三部曲

  • 确定递归参数，返回值
1
2
3
4
5
6
7
8
9
10
11
List<List<String>> res = new ArrayList<>();
List<String> path  = new ArrayList<>();
public List<List<String>> partition(String s) {
    backTracking(s, 0);
    return res;
}

public void backTracking(String s ,int index){
    
}
  • 递归终止条件

只有切割完毕才会收集

1
2
3
4
if(index >= s.length()){
    res.add(new ArrayList<>(path));
    return;
}
  • 单层递归逻辑
1
2
3
4
5
6
7
8
9
10
11
for(int i = index ; i < s.length() ; i++){
    //切割字符串，然后判断字符串是否是回文串， 如果不是，那么就跳过本次的循环，直接进行下一轮
    String str = s.substring(index,i);
    if(isPalindrome(str,index,i + 1)){
        path.add(str);
    }else{
        continue;
    }
   	backTracking(s,i+1);
    path.remove(path.size() - 1);
}

子集问题

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]