300 最长递增子序列

题目：

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

1
2
3
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

1
2
输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

1
2
输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

  • 1 <= nums.length <= 2500
  • -104 <= nums[i] <= 104

进阶：

  • 你能将算法的时间复杂度降低到 O(n log(n)) 吗?

思路：

本题刚开始其实我是按照双指针做的， 当时看到这道题想都没想 直接通过滑动窗口的方式确定最大的递增子序列。 结果看来用例才发现他找的是子序列， 不是连续子序列……

所以滑动窗口的方式基本是不适用这道题的（就算适用我也没想出来思路）。 老老实实按照动态规划的思路

dp[i] 表示 i 之前的最长递增子序列的长度是dp[i]

因为数组的长度最小是1， 并且无论怎么比， 最小的递增子序列长度肯定是1的。因为每个数都有可能是做最长子序列。所以就需要将dp数组全部初始化为1.

然后通过两层for循环遍历， 外层遍历 nums数组中的数， 内层从 0 到 i - 1中找最长子序列。 没遍历完一次都需要更新最长子序列的长度。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int lengthOfLIS(int[] nums) {
        //dp[i] 表示  i 之前的最长递增子序列的长度是dp[i]
        int []dp = new int[nums.length];
        //因为数组大的长度最短都是1 ， 所以一定有一个最长的子序列
        Arrays.fill(dp,1);
        int max = 1;
        for(int i= 0; i< nums.length; i++){
            for(int j = 0; j <i; j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i] ,dp[j] +1);
                }
            }
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}

674 最长连续递增子序列

题目：

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

1
2
3
4
输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2：

1
2
3
输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示：

  • 1 <= nums.length <= 104
  • -109 <= nums[i] <= 109

思路

和上道题一样， 可以使用动态规划， 但是这道题最好的方法还是使用贪心算法，通过局部最优推导出全局。 但是核心思路都是一样的。没啥难的， 通过对比是否nums[i] > nums[i-1] ，如果是， 那就累加即可。最后通过Math.max()得到最大的即可。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int findLengthOfLCIS(int[] nums) {
        //贪心算法实现
        int count = 1;
        int res= 1;
        for(int i =1; i < nums.length; i++){
            if(nums[i] > nums[i-1]){
                count++;
            }else{
                count = 1;
            }
            res = Math.max(res, count);
        }
        return res;

    }
	//动态规划的方法
    /**
      public int findLengthOfLCIS(int[] nums) {
        //dp[i]  表示 i 之前的最长连续子序列长度为 dp[i]
        int []dp = new int[nums.length];
        Arrays.fill(dp,1);
        int res = 1;
        for(int i =1 ;i< nums.length; i++){
            if(nums[i] > nums[i-1]){
                dp[i] = dp[i-1] + 1;
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }
     */
}

718 最长重复数组

题目：

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

示例 1：

1
2
3
输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

1
2
输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

  • 1 <= nums1.length, nums2.length <= 1000
  • 0 <= nums1[i], nums2[i] <= 100

思路

对于本题， 我首先想到的是暴力解法， 两层for循环一一对比， 如果上一个也相同 那么就进行累加，再对累加的结果取最大值。 当然这个思路是没问题， 但是最后也一定会超时。

之后顺着代码随想录的动态规划思维， 按照动态规划的思维重新思考

  1. dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。(“以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )

因为dp[i][j]: 是要通过上一个dp[i-1][j-1]推导出来的。 这是动态规划的本质， 每一步都是由上一步推导。所以我们需要考虑到上一步，所以dp的就是从(1，1) —> (dp[i-1][j-1],dp[i-1][j-1]) 。

如果实在理解 可以通过打印dp数组来进行分析

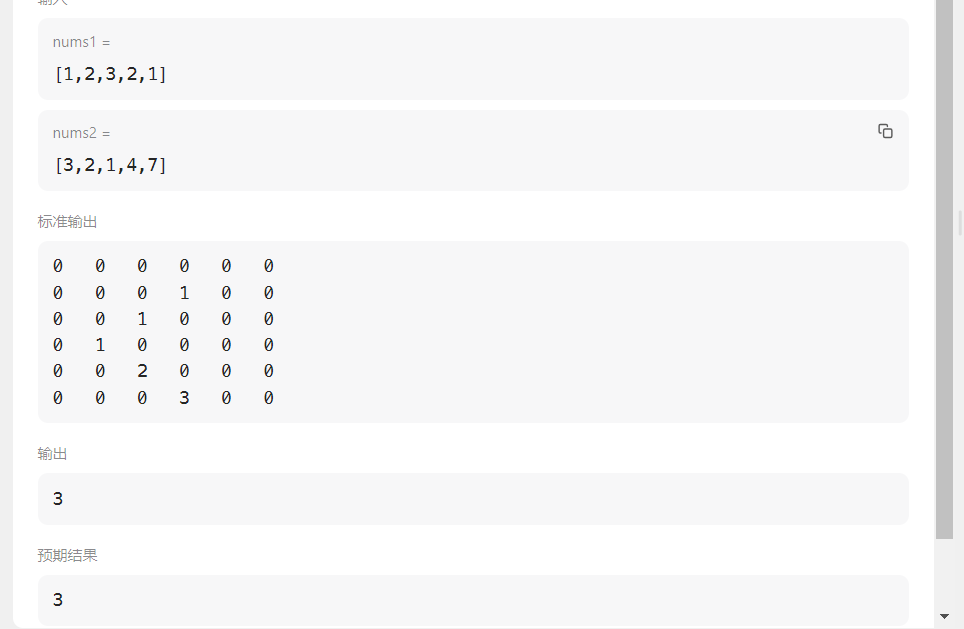
image-20230919141227475

中间的标准输出 就是dp数组的结果。

  1. 对于dp数组的初始化， 这里可以初始化称为0 ， 因为每一步都是通过上一步推导出来的， 如果本次的nums1[i] ==nums2[j] 那么就以上次的结果 + 1 就是这两次的次数。

两层for循环遍历即可。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int res = 0;
        //dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。
        int [][]dp = new int[nums1.length+1][nums2.length+1];
        for(int i= 1; i <= nums1.length ;i++){
            //nums1[i] 对比nums2[j]中的每一个
            for(int j = 1; j <= nums2.length ;j++){
                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                res = Math.max(res, dp[i][j]);
            }
        }

        for(int i= 0 ; i <= nums1.length ;i++){
            for(int j =0 ; j<= nums2.length;j++){
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println();
        }
        return res;
    }
}