392 判断子序列

题目：

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，”ace”是”abcde”的一个子序列，而”aec”不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

示例 1：

输入：s = “abc”, t = “ahbgdc” 输出：true

示例 2：

输入：s = “axc”, t = “ahbgdc” 输出：false

提示：

  • 0 <= s.length <= 100
  • 0 <= t.length <= 10^4
  • 两个字符串都只由小写字符组成。

思路

本题其实不使用动态规划的思路也是能够解出来的 ，并且时间复杂度 和 空间复杂度更低。 因为题目中问的是 s 是否为t 的自序列， 我们自需要顺序遍历 t ，然后对比是否 s中也出现， 并且相对顺序不能变更即可。 代码实现中有。

如果使用·动态规划思路还是那个思路， 只是最后需要对比是否相同在自序列的长度 == s的长度即可。

还有就是在遍历的时候 如果

1
2
3
4
if(s.charAt(i-1) ！= t.charAt(j-1)){
    //相当于t要删除元素，继续匹配
    dp[i][j] = dp[i][j-1];
}

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public boolean isSubsequence(String s, String t) {
        //dp[i] 表示 容量为 i 的数组， 看是否能被填满 
        //i 为子序列 s 填充物为 t 要求保持相对顺序不变
        // int []dp = new int[s.length() + 1];
        if(s.length() == 0 && t.length() >=0 ) return true;
        if(s.length() ==0 || t.length() == 0) return false;
        if(s.length() > t.length()) return false;
        int j =0 ;
        for(int i= 0 ;i < t.length(); i++){
            if(s.charAt(j) == t.charAt(i)){
                j++;
                if(j == s.length()) break;
            }
        }   
        if(j == s.length()){
            return true;
        }
        return false;

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean isSubsequence(String s, String t) {
        //dp[i][j] 表示 下标为 i-1的字符串s 和 下标为 j-1的字符串t 他们相同子序列的长度为 dp[i][j]
        int [][]dp = new int[s.length() +1][t.length() + 1];
        int res=  0;
        for(int i =1; i <= s.length() ;i++){
            for(int j = 1; j <= t.length();j++){
                if(s.charAt(i-1) == t.charAt(j-1)){
                    dp[i][j] =  dp[i-1][j-1] + 1;
                }else{
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        return dp[s.length()][t.length()] == s.length();

    }
}

115 不同的子序列

题目 ：

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数，结果需要对 109 + 7 取模。

示例 1：

1
2
3
输入：s = "rabbbit", t = "rabbit"
输出：3
解释： 如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。 rabbbit rabbbit rabbbit

示例 2：

1
2
输入：s = "babgbag", t = "bag" 输出：5
解释： 如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。  babgbag babgbag babgbag babgbag babgbag

提示：

  • 1 <= s.length, t.length <= 1000
  • s 和 t 由英文字母组成

思路：

按照题目中的问题来定义dp数组的含义。

dp[i][j] 表示 长度为i-1 的 s的自序列 在长度为 j-1 的t中出现的次数其实为啥这样定义我也是有点云里雾里的， 但是按照动态规划的思路， 自然而然你就会往这方面去向想。 然后再按照递归五部曲的顺序去思考每一步的实现可能性， 最后再写即可。

定义出来了， 但是本题还是有问题， 因为不太清楚如何确定递推公式。

如果s[i-1] == t[j-1]那么dp数组该如何进行遍历。 如果不相等 那又该如何 ？

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。

一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]。

一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。 为什么不用 ，因为我们要实现的是s中 t 的个数。只需要考虑s删除某个字符的问题， 而不需要考虑t .如下图

同理不相等的时候 也是这样思考。

img

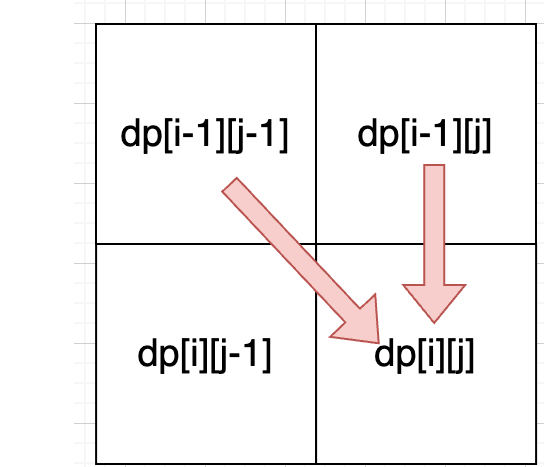
通过上图我们可以看出， dp[i][j] 是由上方 和 dp[i-1][j-1] 推导出来的， 所以需要对其进行初始化赋值

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int numDistinct(String s, String t) {
        int [][]dp = new int[s.length() + 1][t.length()+1];
        //dp[i][j]  表示 长度为i-1 的 s的自序列 在长度为 j-1 的t中出现的次数
        for(int i =0 ;i < s.length();i++) {
            dp[i][0] = 1;
        }


        for(int i =1 ; i <= s.length(); i++){
            for(int j= 1 ; j <= t.length(); j++){

                if(s.charAt(i-1) == t.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1]  + dp[i-1][j];
                }else{
                    //我们这里考虑的是s中有多个t的问题， 所以只需要删除t中的进行比较
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        return dp[s.length()][t.length()];
    }
}

583 两个字符串的删除操作

题目：

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步 可以删除任意一个字符串中的一个字符。

示例 1：

输入: word1 = “sea”, word2 = “eat” 输出: 2 解释: 第一步将 “sea” 变为 “ea” ，第二步将 “eat “变为 “ea”

示例 2:

输入：word1 = “leetcode”, word2 = “etco” 输出：4

提示：

  • 1 <= word1.length, word2.length <= 500
  • word1 和 word2 只包含小写英文字母

思路

按照题目中的要求 ，通过dp数组来对问题进行定义

1
dp[i][i] 表示 字符串长度为i-1的word1 和 字符串长度为 j-1 的word2， 如果想要两个字符串相等， 所需要的最小步数为dp[i][j]

如此就会出现两种情况。

如果**word1.charAt(i-1) == word2.charAt(j-1)**dp数组如何推导

按照之前的递推思路， 那么就是通过dp[i-1][j-1]从而得到dp[i][j]， 因为题目中要求得到的是最小步数，所以这里需要进行 + 1操作

如果**word1.charAt(i-1) != word2.charAt(j-1)**dp数组如何推导

不相等的时候就可以通过之前删除word中的字符时所用到的最小步数来推导 。如图

img

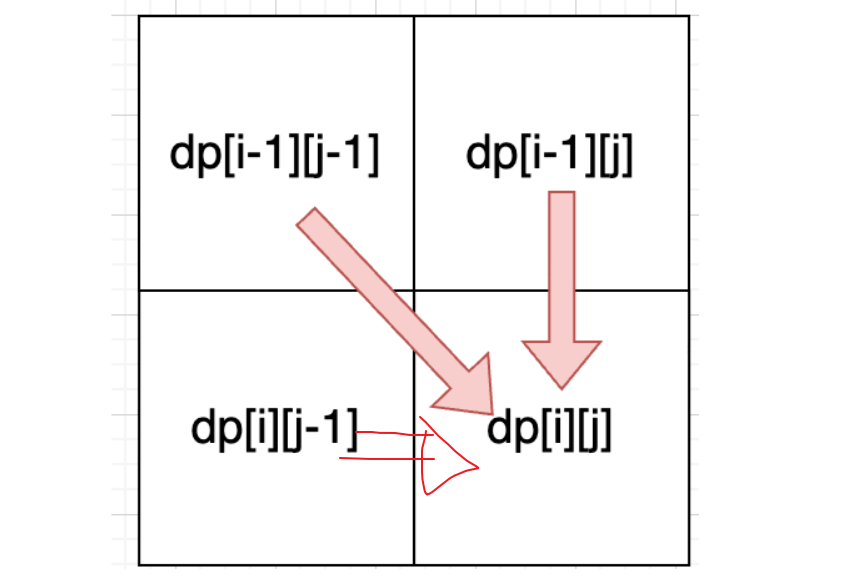
比较：dp[i][j-1]和 dp[i-1][j] 二者通过删除字符 使之相同所需要的最少步数的最小值来获取， 然后最小值 + 1 就是需要的dp[i][j]

初始化

dp[i][0] 表示word2的长度为0 ，word1的长度为i ，如果想要两者相同， 所需要的最少步数是dp[i][0]。

所以这里如果想要两者相同， 那么就需要将word1也删除到 长度为 0的情况才行。所以初始化为 dp[i][0] = i ， 同理，dp[0][j]也是 ，如果想要两者相同， 那么就需要进行初始化为 j

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int minDistance(String word1, String word2) {
        //dp[i][j] 表示 单词长度为 i -1 的word1 和单词长度为 j-1的word2 所需要的最少步数为dp[i][j]
        int [][]dp = new int[word1.length() + 1][word2.length() + 1];

        //初始化
        for (int i = 0; i <= word1.length(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.length(); j++) dp[0][j] = j;
        //确定递推公式
        //如果w1[i] == w2[j]的时候
        //如果w1[i] != w2[j]的时候
        for(int i =1 ; i <= word1.length(); i++){
            for(int j = 1; j <= word2.length();j++){
                if(word1.charAt(i-1) == word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = Math.min(dp[i-1][j] + 1, dp[i][j-1] +1);
                }
            }
        }
        return dp[word1.length()][word2.length()];

    }
}