题目描述

图片描述

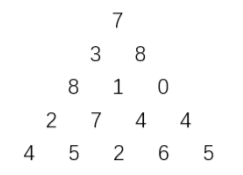
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右 边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

输入描述

输入的第一行包含一个整数 N (1≤N≤100)N (1≤N≤100)，表示三角形的行数。

下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。

输出描述

输出一个整数，表示答案。

输入输出样例

示例

输入

1
2
3
4
5
6
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

输出

1
27

思路

这道题是我刷代码随想录以来第一道现实中出现的题， 刚开始拿到题没什么思路 。所以就学着Carl慢慢一步一步分析，虽然最后思路是对的 ，但是实现起来很多的代码细节还是没有完全掌握 。所以写出来记一记

首先我们可以知道 ，它的每一个路径的起源都是从上一条路径得到的，那么就可以得出使用dp的想法

其次 ，题目中提及路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右 边的那个数。 所以我们的公式就可以从这里推出。

1
2
//从这里我们就可以知道
dp[i][j] : 表示 在第 i 行， 第 j 列 ，我们可以得到的最大的和为 dp[i][j]

以上就是我推断出的dp数组的含义

接下来就是dp的初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//1. dp[0][0] 一定要初始化成为arr的第一个 ，因为后序，我们会用到
dp[0][0] = arr[0][0];

//2. 接下来我们还需要用到dp[i][0] 也就是每一行的第一个，它等于
for(int i =1 ;i < size;i++){
    dp[i][0] = arr[i][0] +  dp[i-1][0];
}
//因为如果我们只对dp[0][0] 进行初始化的话， 那么后序 的dp[2][2] 就需要dp[1][1] 和 dp[1][0]；但是我们的dp[1][0]
//确是只能由dp[0][0]得出。同时dp[1][1] 也是只能由dp[0][0] 得出
//所以我们需要将dp[i][0]也进行初始化 通过 dp[i][0] = arr[i][0] +  dp[i-1][0]; 这样我们得到的dp[1][0] 才是由dp[0][0]相加得到的


//3. 接下来就是dp的公式
//因为我们之前推出的公式我们得到了dp[i][0] 的数据
//所以接下来就可以按照题意将其余的dp[i][j] 推出
dp[i][j] = arr[i][j] + Math.max(dp[i-1][j],dp[i-1][j-1]);
//所以就可以得到上述公式

//4. 遍历顺序
for(int i = 1;i < size;i++){
    for(int j =1;j <= i;j++){
        dp[i][j] = arr[i][j] + Math.max(dp[i-1][j],dp[i-1][j-1]);
    }
}

经过这样的推导 ，我们就可以得出需要dp数组 ，但是题目中还规定了向左下走的次数与向右下走的次数相差不能超过 1。 那么我们就不能直接得出最后一个(sp[N][N])的结果。 最终的结果一定是在其中间 所以进行判断一下即可

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int size = scan.nextInt();
        int[][] arr = new int[size][size];
        for(int i = 0;i < size;i++){
          for(int j = 0;j <= i;j++){
            arr[i][j] = scan.nextInt();
          }
        }
        scan.close();
        //定义dp
        int[][] dp = new int[size][size];
        dp[0][0] = arr[0][0];
        //初始化dp
        for(int i =1 ;i < size;i++){
          dp[i][0] = arr[i][0] +  dp[i-1][0];
        }
        //确定dp公式及其遍历顺序
        for(int i = 1;i < size;i++){
          for(int j =1;j <= i;j++){
            dp[i][j] = arr[i][j] + Math.max(dp[i-1][j],dp[i-1][j-1]);
          }
        }
        
        if(size%2 != 0 ){
          System.out.println(dp[size - 1][size/2]);
        }else{
          System.out.println(Math.max(dp[size-1][size/2], dp[size-1][size/2-1]));  
        }
    }
}