二叉树题目合集

求二叉树是否相同？

用递归法 ，传入左右两棵树的根节点 ，然后比较 left.left == right.left; 以及 left.right ==right.right;

这是递归里面的内容

递归结束的条件：

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if( p == null && q == null){
    	    return true ; // 这样的情况下就可以返回true了
        }else if ( p != null && q == null){
            return false;
        }else if( p == null && q != null ){
            return false;
        }else if (p.val != q.val){
            return false;
        }else{

            //递归的内容
            boolean b1 = isSameTree(p.left , q.left);
            boolean b2 = isSameTree(p.right ,q.right);
            boolean b = b1 && b2;
            return b;
        }  
    }
}

求二叉树是否对称 ？

class Solution {
    //这里我们用队列来实现，思路： 
        //将左右子树分开，然后分别以左右为树比较
    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }else{
            return isTrue(root.left , root.right);
        }
    }
    public boolean isTrue(TreeNode left, TreeNode right){
        if(left == null && right == null){
            return true;
        }else if(left == null || right == null){
            return false;
        }else if(left.val != right.val ){
            return false;
        }
        else{
            return isTrue(left.left,right.right) && isTrue(left.right , right.left);
        }
    }
}

求完全二叉树的节点数

方法一 ： 最原始的方法， 用迭代法或者递归的方法将二叉树遍历完，得出节点的数量

方法二 ： 只针对完全二叉树的解法

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

按照这个完全二叉树的特征。我们就可以确定一个终止条件

if(leftDepth == rightDepth){
	return 2<<leftDepth - 1;
}

完全二叉树只有两种情况

情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

1. 对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
2. 对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来 计算。

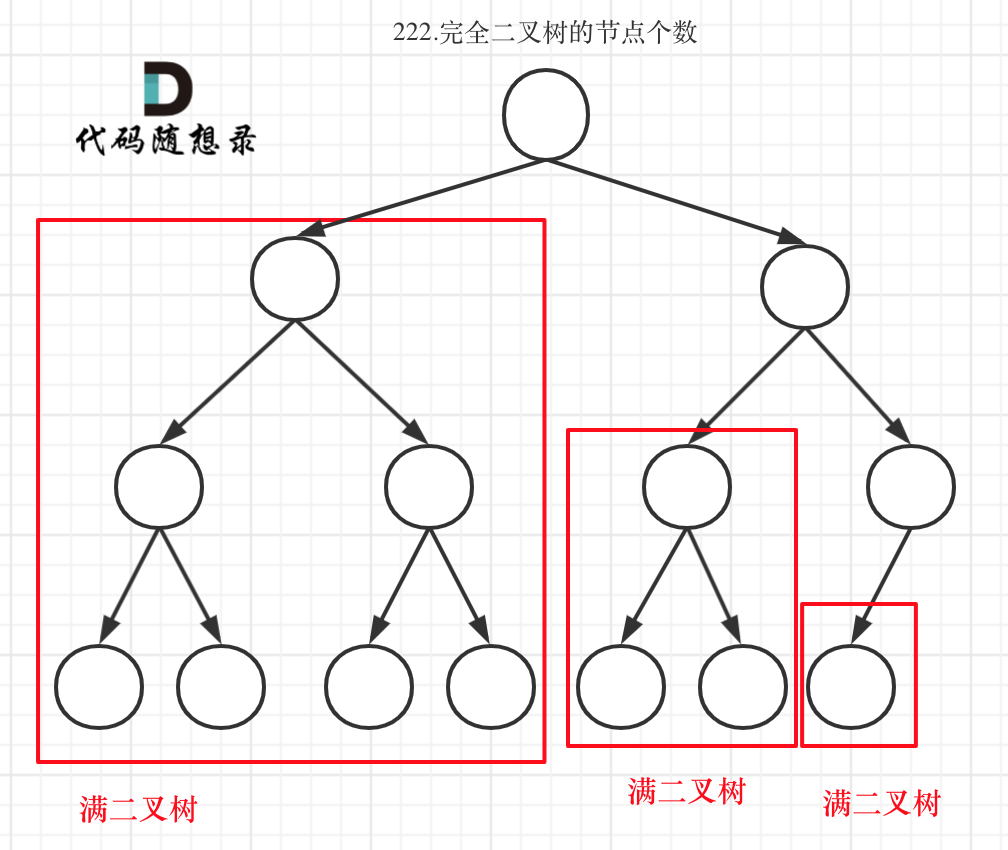
所以说如果整棵树不是满二叉树的话，那么就递归他的左右孩子，直到递归到某棵子树 ，它（子树）是满二叉树， 那么就达到递归截至的条件 ，输出节点数。

class Solution {
    public int countNodes(TreeNode root) {
        if(root == null){
            return 0;
        }
        TreeNode leftD = root.left;
        TreeNode rightD = root.right;
        int rD = 0;
        int lD = 0;//初始化为0 是为了后面求指数方便

    	//求左右子树的深度
        while(leftD != null){
            leftD = leftD.left;
            lD++;
        }
        while(rightD != null){
            rightD = rightD.right;
            rD++;
        }
    	//如果判断该树是满二叉树那么直接输出即可
        if(rD == lD){
            return (2 << lD) - 1; // 2^n - 1
        }

    	//继续递归，计算完左右子树的节点，然后再加上根节点;
        lNum = countNodes(root.left);
        rNum =  countNodes(root.right);
        return lNum + rNum + 1;
    }
}

总结 ：对于这个二叉树来说，他没有遍历所有的节点，如果说一个节点的子树他是满二叉树，那么就只需要用2 << n - 1这个公式就能算出这个子树的所有节点。

平衡二叉树

一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

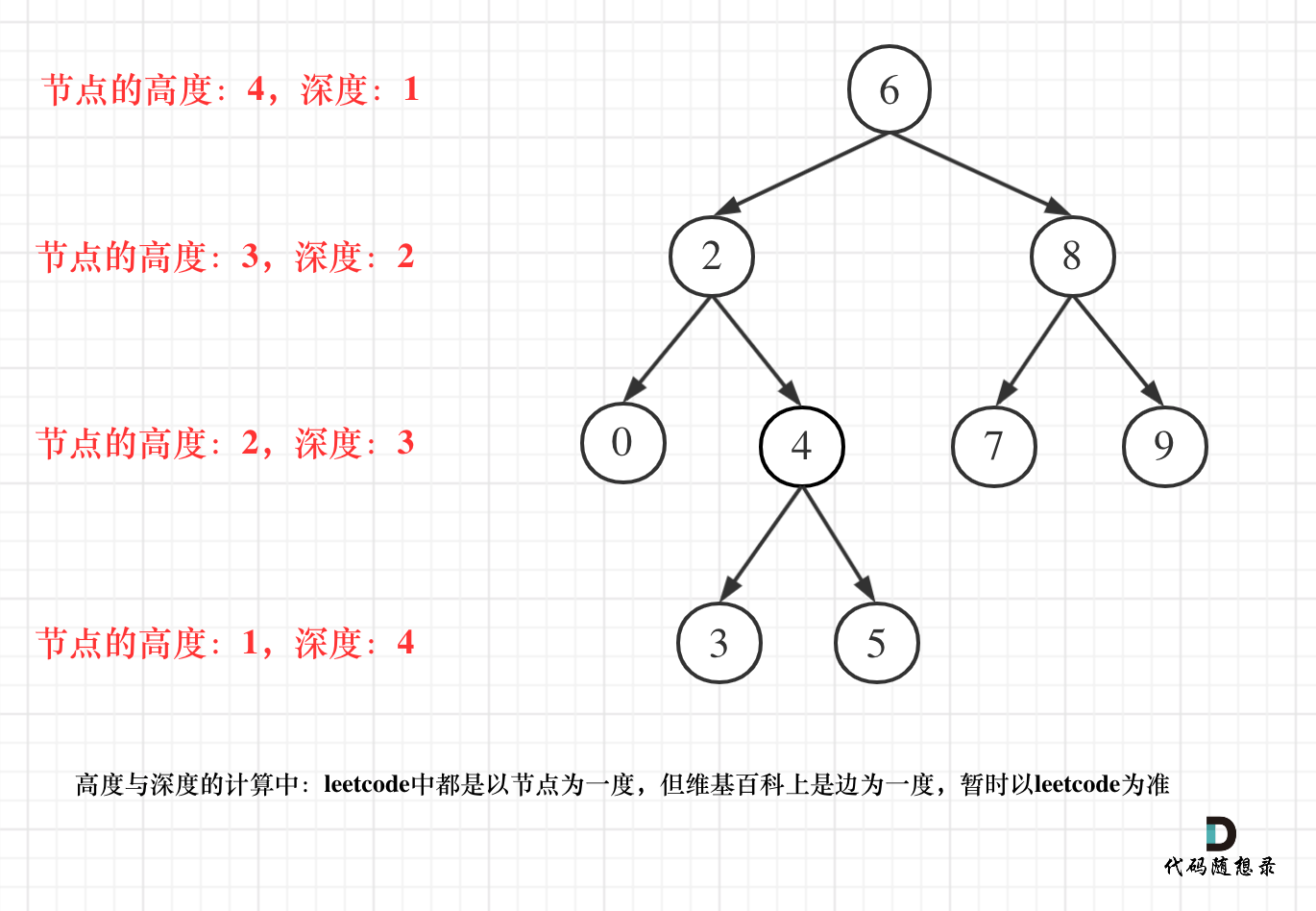
• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

求解高度用后序遍历 ， 求解深度用前序遍历

【因为后序是根据左右孩子的高度，然后父节点再根据左右孩子节点的情况进行 + 1 ===》》》层层向上返回 】

【前序求解的深度 ，顺序是 [中左右]一直向下遍历，不向上返回结果。符合一直向下统计节点的深度 】

class Solution {
    public boolean isBalanced(TreeNode root) {
        int res = isTree(root);
        return res == -1 ? false : true;
    }
    //先定义一个方法判断平衡二叉树
    public int isTree(TreeNode node){
        if(node == null){
            return 0;
        }
        int ll = isTree(node.left);
        if(ll == -1){
            return -1;
        }
        int rl = isTree(node.right);
        if(rl == -1){
            return -1;
        }
        //判断是否满足平衡二叉树的条件
        if(Math.abs(ll-rl) > 1){
            return -1;
        }
        //返回平衡二叉树的高度
        return Math.max(ll,rl) + 1;
    }
}

求解深度的方法(c++ 实现)

class Solution {
public:
    int result;
    void getDepth(TreeNode* node, int depth) {
        result = depth > result ? depth : result; // 中

        if (node->left == NULL && node->right == NULL) return ;

        if (node->left) { // 左
            depth++;    // 深度+1
            getDepth(node->left, depth);
            depth--;    // 回溯，深度-1
        }
        if (node->right) { // 右
            depth++;    // 深度+1
            getDepth(node->right, depth);
            depth--;    // 回溯，深度-1
        }
        return ;
    }
    int maxDepth(TreeNode* root) {
        result = 0;
        if (root == 0) return result;
        getDepth(root, 1);
        return result;
    }
};

二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。

在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

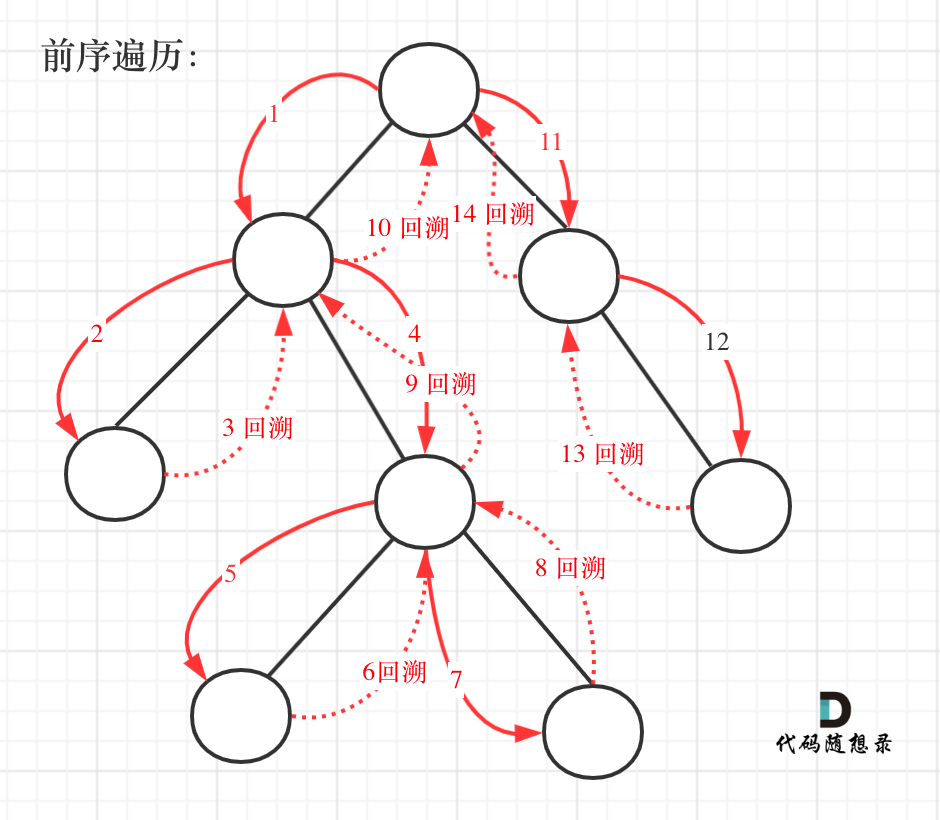
求二叉树的所有路径思路（草图）

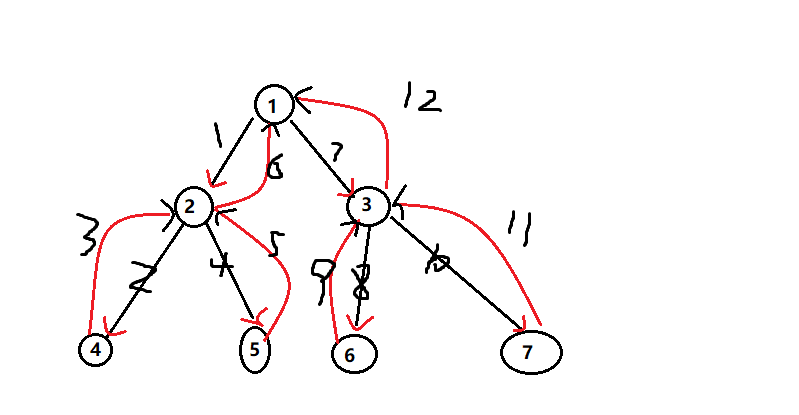
1. 创建路径集合path 以及 结果集合list。用于存储路径与最后的结果
2. 前序遍历 ，先将父节点加入到路径集合path中
3. 递归结束的条件 –> 到叶子节点 （如图的 4 号节点）
4. 递归结束，回溯之前。将该路径保存到结果路径中

class Solution {
    
    public List<String> binaryTreePaths(TreeNode root) {
        //用递归 ，前序遍历
        List<String> list = new ArrayList<>();
        if(root == null){
            return list;
        }
        List<Integer> path = new ArrayList<>(); 
        prefix(root,path,list);
        return list;
    }
    public void prefix(TreeNode node , List<Integer> path, List<String> list){
    	//先将该节点保存到路径
        path.add(node.val);

        //如果到叶子节点就结束本次递归
        if(node.left == null && node.right == null){
            //StringBuffer用于拼接路径
            StringBuffer sb = new StringBuffer();
            //循环拼接路径
            for(int i=0 ;i<path.size() - 1 ;i++){
                //因为当前的节点都已经保存到了path中，所以这里只需要循环按要求拼接即可
                sb.append(path.get(i)).append("->");
            }
            /*
        因为最后循环结束时如果我们将最后一个节点也拼接进入 ，那么势必会多出来一个‘->’这就与题目要求的不符合
    	所以我们将最后一个节点放到循环外面拼接
            */
            sb.append(path.get(path.size()-1)); 
            //将拼接好的路径保存起来
            list.add(sb.toString());
           // 结束本次递归
            return;
        }
        if(node.left != null){
            prefix(node.left , path ,list);
            //递归结束 ，回溯时删除最后一个节点，【1-> 2 -> 5】路径就会变成【1 -> 2 -> 】
        	//这样下次递归就会从【2】节点开始 
            path.remove(path.size() - 1 );
        }
        if(node.right != null){
            prefix(node.right , path , list);
            path.remove(path.size() - 1);
        }
    }
}

获取树最左下角的节点的值

//方法一 ； 递归法

class Solution {
    public int res = 0;
    public int depth =  - 1;
    public int findBottomLeftValue(TreeNode root) {
        if(root == null){
            return 0;
        }
        GetLeft(root,1);
        return res;  
    }
    public void GetLeft(TreeNode root , int deep){
        if(root.left == null && root.right == null){
            if(deep > depth){
                depth = deep;
                res = root.val;
            }  
        }
        if(root.left != null){
            GetLeft(root.left , deep+1);
        }
        if(root.right != null){
            GetLeft(root.right, deep + 1);
        }
    }
}


//方法二 ： 迭代法
 */
class Solution {
    List<List<Integer>> list = new ArrayList<>();
    public int findBottomLeftValue(TreeNode root) {
        if(root == null){
            return 0;
        }
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        while(!que.isEmpty()){
            int size = que.size();
            List<Integer> nodeList = new ArrayList<>();
            for(int i= 0 ;i<size;i++){
                TreeNode node = que.poll();
                nodeList.add(node.val);
                if(node.left != null){
                    que.offer(node.left);
                }
                if(node.right != null){
                    que.offer(node.right);
                }
            }
            list.add(nodeList);
        }
        return list.get(list.size()- 1).get(0);
    }
}

//迭代法二 ： 
//迭代法
class Solution {

    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int res = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();
                if (i == 0) {
                    res = poll.val;
                }
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
            }
        }
        return res;
    }
}

路径总和二

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

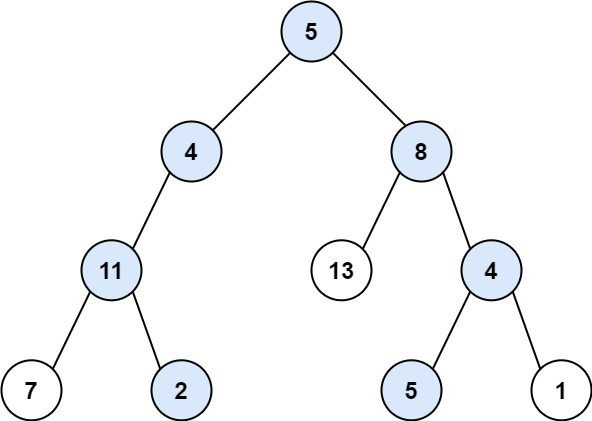
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22

输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

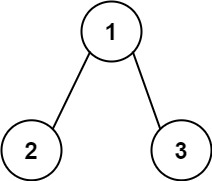
输入：root = [1,2,3], targetSum = 5

输出：[]

示例 3：

输入：root = [1,2], targetSum = 0

输出：[]

class Solution {
    List<List<Integer>> list = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        if(root== null){
            return list;
        }
        List<Integer> path = new ArrayList<>();
         prefix(root,path,targetSum);
        return list;
    }
    public void prefix(TreeNode root, List<Integer> path,int targetSum){
        path.add(root.val);
        if(root.left == null && root.right == null){
            List<Integer> alist= new ArrayList<>();
            for(int i= 0;i<path.size();i++){
                alist.add(path.get(i));
            }
            int size = alist.size();
            int sum = 0;
            for(int j =0;j<size;j++){
                sum += alist.get(j);
            }
            if(sum == targetSum){
                list.add(alist);
            }
        }
        if(root.left != null){
            prefix(root.left , path, targetSum);
            path.remove(path.size()-1);
        }
        if(root.right != null){
            prefix(root.right , path, targetSum);
            path.remove(path.size()-1);
        }
    }
}

从中序与后序构建二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]输出：[3,9,20,null,null,15,7]示例 2:

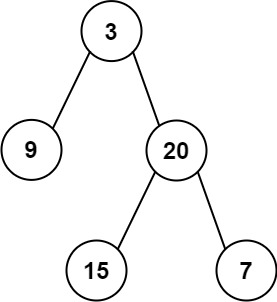
输入：inorder = [-1], postorder = [-1]输出：[-1]

思路

1. 判断数组是否为空 ！
2. 不为空则向下继续，为空返回null
3. 去后序数组中的最后一个元素为树的头节点的val值，（原因由后序遍历可知）
4. 切割中序数组 ，以头节点的val值为区分（作为切割点） ，切割成中序左数组 和 中序右数组
5. 切割后序数组， 切成后序左数组 和后序右数组
6. 递归处理左右区间

思维图

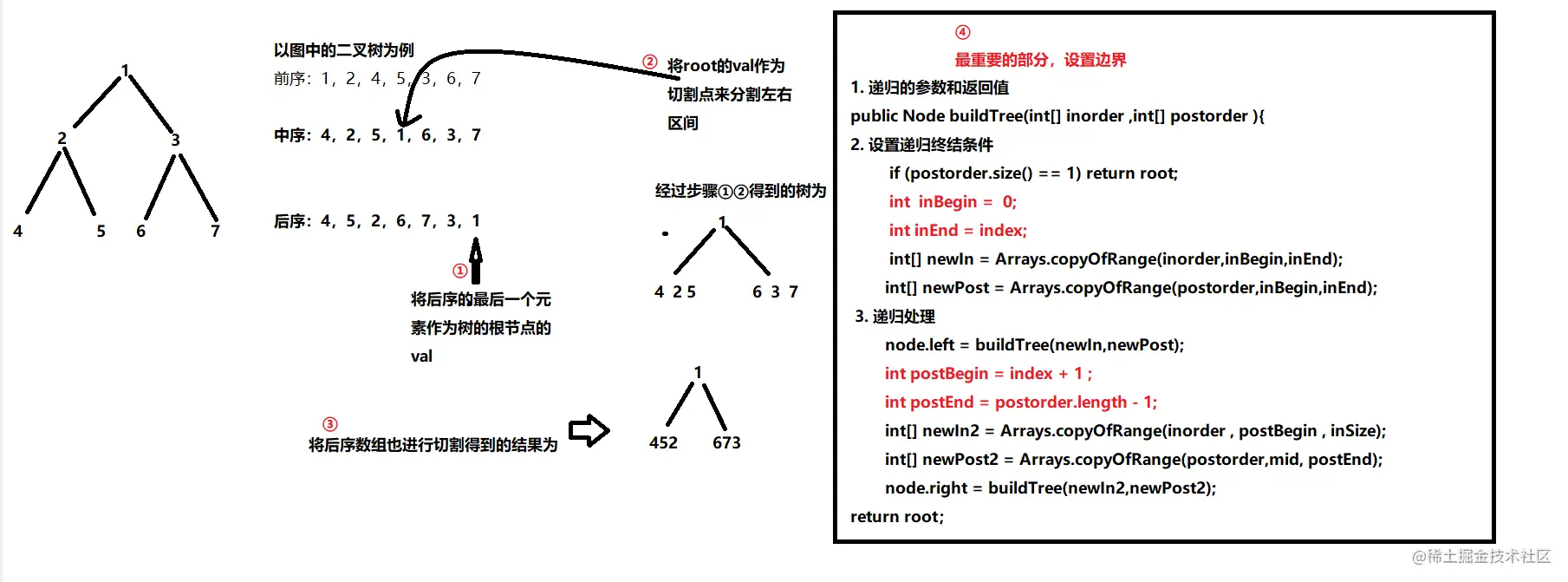
代码实现（复杂易懂）

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if(inorder.length == 0 || postorder.length == 0){
            return null;
        }
        int rootVal = postorder[postorder.length - 1];
        TreeNode node = new TreeNode(rootVal);
        
        int inSize = inorder.length;
        int postSize = postorder.length;
        
        int mid; 
        for(mid = 0; mid < inSize;mid++){
            if(inorder[mid] == rootVal){
                break;
            }
        }
        //切割中序
        int inBegin =  0;
        int inEnd = mid;
        int[] newIn = Arrays.copyOfRange(inorder,inBegin,inEnd);
        int[] newPost = Arrays.copyOfRange(postorder,inBegin,inEnd);
        node.left = buildTree(newIn,newPost);

        int postBegin = mid + 1 ;
        int postEnd = postorder.length - 1;
        int[] newIn2 = Arrays.copyOfRange(inorder , postBegin , inSize);
        int[] newPost2 = Arrays.copyOfRange(postorder,mid, postEnd);
        node.right = buildTree(newIn2,newPost2);
        return node;
    }
}

代码实现（简易map版）

class Solution {
    Map<Integer, Integer> map;  // 方便根据数值查找位置
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
            map.put(inorder[i], i);
        }

        return findNode(inorder,  0, inorder.length, postorder,0, postorder.length);  // 前闭后开
    }
    
    public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
        // 参数里的范围都是前闭后开
        if (inBegin >= inEnd || postBegin >= postEnd) {  // 不满足左闭右开，说明没有元素，返回空树
            return null;
        }
        int rootIndex = map.get(postorder[postEnd - 1]);  // 找到后序遍历的最后一个元素在中序遍历中的位置
        TreeNode root = new TreeNode(inorder[rootIndex]);  // 构造结点
        int lenOfLeft = rootIndex - inBegin;  // 保存中序左子树个数，用来确定后序数列的个数
        root.left = findNode(inorder, inBegin, rootIndex,
                            postorder, postBegin, postBegin + lenOfLeft);
        root.right = findNode(inorder, rootIndex + 1, inEnd,
                            postorder, postBegin + lenOfLeft, postEnd - 1);

        return root;
    }
}

从前序与中序构建二叉树

思路

与从中序和后序构建二叉树相同

代码实现

class Solution {
    Map<Integer, Integer> map;  // 方便根据数值查找位置
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
            map.put(inorder[i], i);
        }

        return findNode(inorder,  0, inorder.length, postorder,0, postorder.length);  // 前闭后开
    }
    
    public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
        // 参数里的范围都是前闭后开
        if (inBegin >= inEnd || postBegin >= postEnd) {  // 不满足左闭右开，说明没有元素，返回空树
            return null;
        }
        int rootIndex = map.get(postorder[postEnd - 1]);  // 找到后序遍历的最后一个元素在中序遍历中的位置
        TreeNode root = new TreeNode(inorder[rootIndex]);  // 构造结点
        int lenOfLeft = rootIndex - inBegin;  // 保存中序左子树个数，用来确定后序数列的个数
        root.left = findNode(inorder, inBegin, rootIndex,
                            postorder, postBegin, postBegin + lenOfLeft);
        root.right = findNode(inorder, rootIndex + 1, inEnd,
                            postorder, postBegin + lenOfLeft, postEnd - 1);

        return root;
    }
}

参考说明（感谢！）：

力扣！

代码随想录！