从中序与后序构建二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
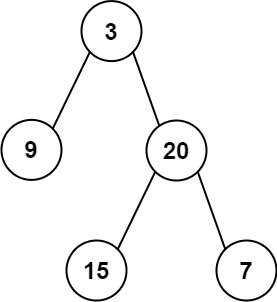
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
思路
- 判断数组是否为空 !
- 不为空则向下继续,为空返回null
- 去后序数组中的最后一个元素为树的头节点的val值,(原因由后序遍历可知)
- 切割中序数组 ,以头节点的val值为区分(作为切割点) ,切割成中序左数组 和 中序右数组
- 切割后序数组, 切成后序左数组 和后序右数组
- 递归处理左右区间
思维图
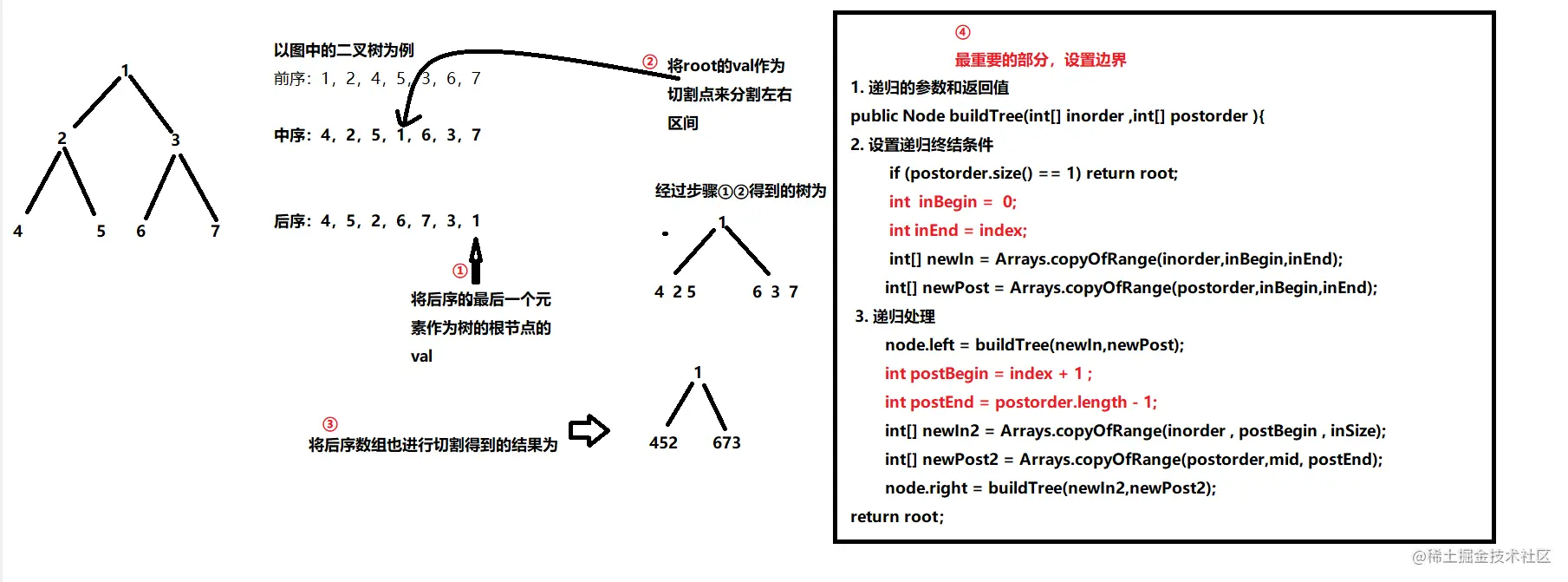
代码实现(复杂易懂)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder.length == 0 || postorder.length == 0){
return null;
}
int rootVal = postorder[postorder.length - 1];
TreeNode node = new TreeNode(rootVal);
int inSize = inorder.length;
int postSize = postorder.length;
int mid;
for(mid = 0; mid < inSize;mid++){
if(inorder[mid] == rootVal){
break;
}
}
int inBegin = 0;
int inEnd = mid;
int[] newIn = Arrays.copyOfRange(inorder,inBegin,inEnd);
int[] newPost = Arrays.copyOfRange(postorder,inBegin,inEnd);
node.left = buildTree(newIn,newPost);
int postBegin = mid + 1 ;
int postEnd = postorder.length - 1;
int[] newIn2 = Arrays.copyOfRange(inorder , postBegin , inSize);
int[] newPost2 = Arrays.copyOfRange(postorder,mid, postEnd);
node.right = buildTree(newIn2,newPost2);
return node;
}
}
|
代码实现(简易map版)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
Map<Integer, Integer> map;
public TreeNode buildTree(int[] inorder, int[] postorder) {
map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return findNode(inorder, 0, inorder.length, postorder,0, postorder.length);
}
public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
if (inBegin >= inEnd || postBegin >= postEnd) {
return null;
}
int rootIndex = map.get(postorder[postEnd - 1]);
TreeNode root = new TreeNode(inorder[rootIndex]);
int lenOfLeft = rootIndex - inBegin;
root.left = findNode(inorder, inBegin, rootIndex,
postorder, postBegin, postBegin + lenOfLeft);
root.right = findNode(inorder, rootIndex + 1, inEnd,
postorder, postBegin + lenOfLeft, postEnd - 1);
return root;
}
}
|
从前序与中序构建二叉树
思路
与从中序和后序构建二叉树相同
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
Map<Integer, Integer> map;
public TreeNode buildTree(int[] inorder, int[] postorder) {
map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return findNode(inorder, 0, inorder.length, postorder,0, postorder.length);
}
public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
if (inBegin >= inEnd || postBegin >= postEnd) {
return null;
}
int rootIndex = map.get(postorder[postEnd - 1]);
TreeNode root = new TreeNode(inorder[rootIndex]);
int lenOfLeft = rootIndex - inBegin;
root.left = findNode(inorder, inBegin, rootIndex,
postorder, postBegin, postBegin + lenOfLeft);
root.right = findNode(inorder, rootIndex + 1, inEnd,
postorder, postBegin + lenOfLeft, postEnd - 1);
return root;
}
}
|
c++版本实现
从中序与后序构建二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
Node* buildTree(vector<int> &inorder , vector<int> &postorder){
if (inorder.size() == 0){
return nullptr;
}
int val = postorder[postorder.size()-1];
Node *root = new Node(val);
int index ;
for(index= 0; index < inorder.size();index++){
if (inorder[index] == val){
break;
}
}
vector<int> leftIn(inorder.begin(),inorder.begin() + index);
vector<int> rightIn(inorder.begin() + index + 1,inorder.end());
postorder.resize(postorder.size() - 1);
vector<int> leftPost(postorder.begin(), postorder.begin() + leftIn.size());
vector<int> rightPost(postorder.begin() + leftIn.size() , postorder.end());
root->left = buildTree(leftIn, leftPost);
root->right = buildTree(rightIn , rightPost);
return root;
}
|
从前序与中序构建二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| Node* Build(vector<int> &preorder ,vector<int> &inorder){
if (inorder.size() == 0){
return nullptr;
}
int val = preorder[0];
Node * root = new Node(val);
int index;
for(index = 0;index < inorder.size();index++){
if (val == inorder[index])
break;
}
for (int i = 1; i < preorder.size(); ++i) {
preorder[i - 1] = preorder[i];
}
preorder.resize(preorder.size() - 1);
vector<int> leftIn(inorder.begin(), inorder.begin() + index);
vector<int> rightIn(inorder.begin() + index + 1,inorder.end());
vector<int> leftPre(preorder.begin() , preorder.begin() + leftIn.size());
vector<int> rightPre(preorder.begin() + leftIn.size() , preorder.end());
root->left = Build(leftPre,leftIn);
root->right = Build(rightPre, rightIn);
return root;
}
|
主函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| int main(){
int arr[] = {1, 2, 3, 4, 5};
int size = sizeof(arr) / sizeof(arr[0]);
vector<int> vec(arr, arr + size);
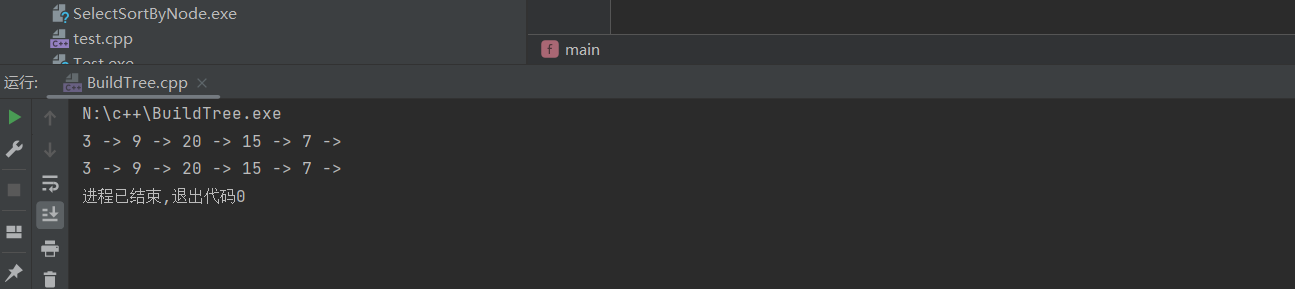
vector<int> preorder = {3,9,20,15,7};
vector<int> inOrder = {9,3,15,20,7};
vector<int> postOrder = {9,15,7,20,3};
Node* root = buildTree(inOrder,postOrder);
Node* root1 = Build(preorder,inOrder);
preOrder(root1);
preOrder(root);
return 0;
}
|
参考说明(感谢!):
力扣!
代码随想录!











