参考 : 代码随想录

img

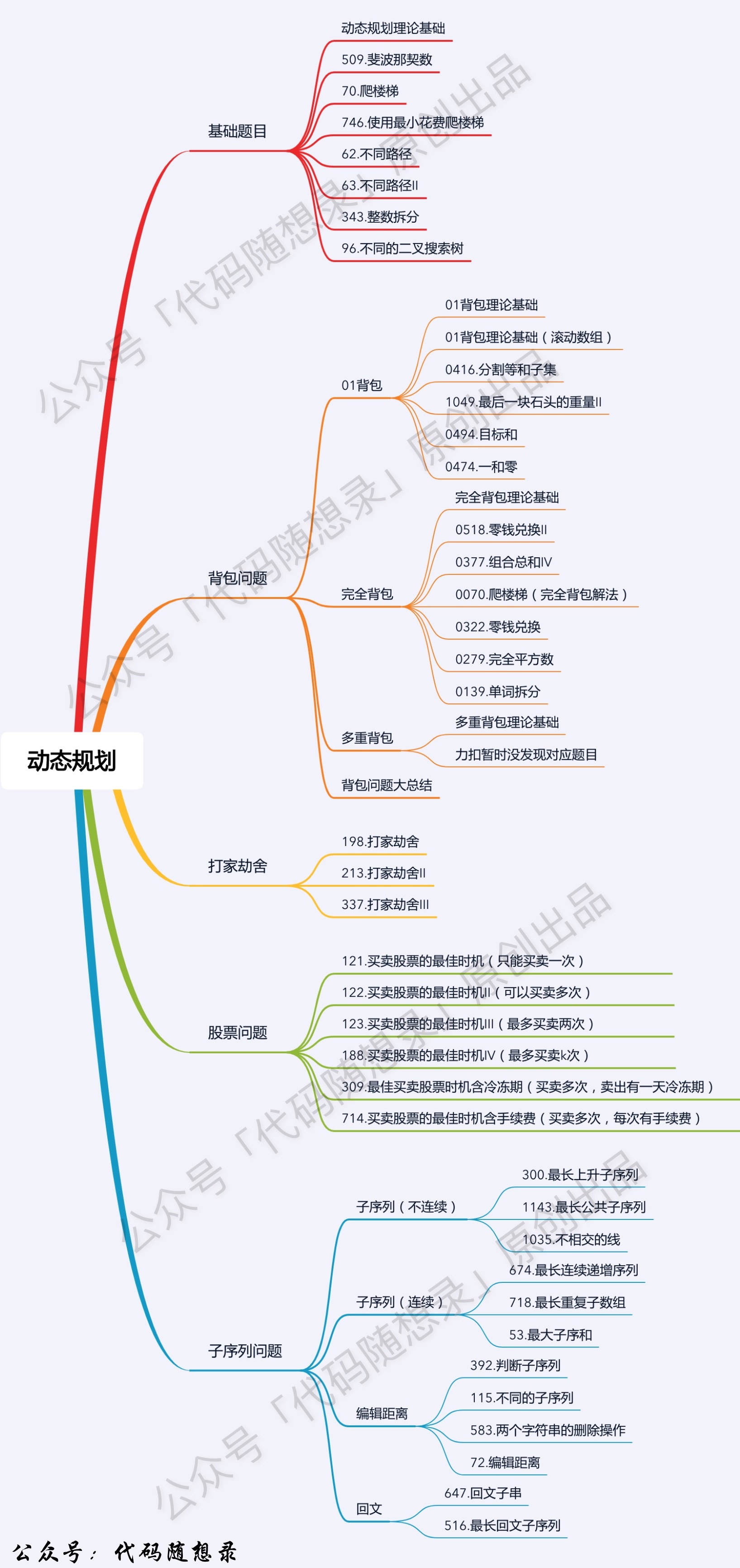
理论知识

动态规划问题，将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

  1. 确定dp数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

发出这样的问题之前，其实可以自己先思考这三个问题：

  • 这道题目我举例推导状态转移公式了么？
  • 我打印dp数组的日志了么？
  • 打印出来了dp数组和我想的一样么？

如果这灵魂三问自己都做到了，基本上这道题目也就解决了

01背包问题

详解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
/**
 *  0 1背包问题
 *有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。
 * 每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
 */
public class beibao {

    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testWeightBagProblem(weight,value,bagSize);
    }

    /**
     * 动态规划获得结果
     * @param weight 物品的重量
     * @param value 物品的价值
     * @param bagSize 背包的大小
     */
    public static void testWeightBagProblem(int[] weight , int[] value, int bagSize){
        //动归五部曲
        //todo 1. 确定dp数组的意义
        //dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
        int[][] dp = new int[weight.length][bagSize + 1];

        //todo 2. 确定递推公式
        /*
         * dp[i][j] = max(dp[i-1][j],dp[i-1][j - weight[i]] + value[i])
         * 由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。
         *
         * 由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，
         *      那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
         */

        //todo 3. 初始化dp
        /*
         * 首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。
         *  有dp方程可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。
         *  dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。
         *
         *  那么很明显
         *          当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。
         *          当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品
         *
         * dp[0][j] 和 dp[i][0] 都已经初始化了，那么其他下标应该初始化多少呢？
         *    其实从递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
         *    可以看出dp[i][j] 是由左上方数值推导出来了，那么 其他下标初始为什么数值都可以，因为都会被覆盖
         *
         */
        for(int j =weight[0]; j <= bagSize;j++){
            dp[0][j] = value[0];
        }

        //todo 4. 遍历的顺序
        for(int i =1;i < weight.length;i++){

            for(int j = 1 ; j <= bagSize;j++){
                //如果背包容量小于物品大小，直接跳过
                if(j < weight[i]){
                    dp[i][j] = dp[i-1][j];
                }else{
                    /*
                     * 当前背包的容量可以放下物品i
                     * 那么此时分两种情况：
                     *    1、不放物品i
                     *    2、放物品i
                     * 比较这两种情况下，哪种背包中物品的最大价值最大
                     */
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - weight[i]] + value[i]);
                }
            }
        }

        //todo 5. 打印结果
        for(int i = 0;i< dp.length;i++){
            for(int j =0 ;j< dp[0].length;j++){
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println();
        }

    }
}

优化: 使用一维数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
package First;

import java.util.*;

/**
 * 使用一维数组代替二维数组
 */
public class yiweibeibao {
    public static void main(String[] args) {
        int[] weight = {1,3,4,5,6,8};
        int[] value = {15,20,30,40,45,20};
        int bagSize = 4;
        WeightBagProblem(weight,value,bagSize);
    }

    /**
     * 使用一维数组写出背包问题
     * @param weight 物体的重量   [i]索引代表物体编号
     * @param value 物品的价值 [i] 索引代表物体编号
     * @param bagSize 背包的大小
     */
    public static void WeightBagProblem(int[] weight, int[] value, int bagSize) {
        //todo 1. 确定dp数组的含义
        //容量为j的背包，所背的物品价值可以最大为dp[j]。
        int[] dp = new int[bagSize + 1];
        //todo 2. 确定递推公式
        //dp[j] =  max(dp[j],dp[j - weight[i]])
        //todo 3. 初始化dp数组
       //dp[0] = 0;       其实初始化和不初始化都一样
        //todo 4. 确立好遍历顺序 
        for(int i =0 ;i < weight.length;i++){
            //从尾到头遍历，  避免重复添加物品
             // 当物品的重量  >  当前背包的容量时 停止添加
            for(int j=bagSize ;j >= weight[i];j--){
                dp[j] = Math.max(dp[j] , dp[j - weight[i]] + value[i]);
                System.out.println(Arrays.toString(dp));
            }
            System.out.println();
        }
        //todo 5. 打印结果
        for (int j = 0; j <= bagSize; j++){
            System.out.print(dp[j] + " ");
        }
    }
}

运行结果

image-20230310180708966